Question

【题目】如图，抛物线与轴交于、两点，与轴交于点，且．

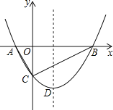
（1）求抛物线的解析式和顶点的坐标；

（2）判断的形状，证明你的结论；

（3）点是轴上的一个动点，当的周长最小时，求的值．

Answer 1

【答案】（1）点坐标为；（2）为直角三角形；（3）

【解析】

（1）把A点坐标代入可求得b的值，可求得抛物线的解析式，再求D点坐标即可；

（2）由解析式可求得A、B、C的坐标，可求得AB、BC、AC的长，由勾股定理的逆定理可判定△ABC为直角三角形；

（3）先求得C点关于x轴的对称点E，连接DE，与轴交于点M，则M即为所求，可求得DE的解析式，令其y=0，可求得M点的坐标，可求得m．

解：（1）∵点在抛物线上，

∴，解得，

∴ 抛物线解析式为，

∵ ，

∴ 点坐标为；

（2）为直角三角形，证明如下：

在中，令可得，解得或，

∴ 为，且为，

∴ ，，，

由勾股定理可求得，，

又，

∴ ，

∴ 为直角三角形；

（3）∵ ，

∴ 点关于轴的对称点为，

如图，连接，交轴于点，则即为满足条件的点，

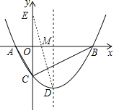
设直线解析式为，

把、坐标代入可得，解得，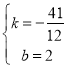

∴ 直线解析式为，令，可得，

∴ ．