��Ŀ����
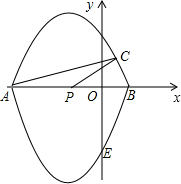 ��ͼ����ƽ��ֱ������ϵxOy�У�������A��C��B�������ߵ�һ�����뾭����A��E��B�������ߵ�һ������ϳ�һ��������ߣ����ǰ�����������߳�Ϊ��˫�����ߡ�����֪PΪAB�е㣬��P��-1��0����C��
��ͼ����ƽ��ֱ������ϵxOy�У�������A��C��B�������ߵ�һ�����뾭����A��E��B�������ߵ�һ������ϳ�һ��������ߣ����ǰ�����������߳�Ϊ��˫�����ߡ�����֪PΪAB�е㣬��P��-1��0����C��| 2 |
��1������˫�����ߡ��о�����A��E��B�������ߵĽ���ʽ��
��2�����һ��ֱ���롰˫�����ߡ�ֻ��һ�����㣬��ô����ֱ�߽�����˫�����ߡ������ߣ�������E��x��ƽ�е�ֱ���롰˫�����ߡ����ڵ�G������G�ġ�˫�����ߡ����ߵĽ���ʽ��
���㣺���κ����ۺ���
ר�⣺
��������1����֪��APC������͵�C�������꣬���ɵõ�AP�ij��������ɸ���P�����꣬���A��B�����꣬�Ӷ����ô���ϵ������ù�A��E��B����������߽���ʽ��
��2������E��G���������ߵĶԳ���Գƣ������G������꣬���������G�����ߵĽ���ʽ������G����������ֱ�ߵĽ���ʽ�У�������ȥһ��δ֪����Ȼ��������1�����������ߵĽ���ʽ��������������ֻ��һ�����㣬��ô���÷��̵ĸ����б�ʽ��=0���ɾݴ���������ߵĽ���ʽ��
��2������E��G���������ߵĶԳ���Գƣ������G������꣬���������G�����ߵĽ���ʽ������G����������ֱ�ߵĽ���ʽ�У�������ȥһ��δ֪����Ȼ��������1�����������ߵĽ���ʽ��������������ֻ��һ�����㣬��ô���÷��̵ĸ����б�ʽ��=0���ɾݴ���������ߵĽ���ʽ��
����⣺��1����S��ACP=
AP•|yC|=1��������֪��|yC|=1��
��AP=2����A��-3��0����
����A��B���ڵ�P�Գƣ���B��1��0����
�辭��A��E��B�������ߵĽ���ʽΪ��y=a��x+3����x-1�������У�
a��0+3����0-1��=-3��a=1��
�����������ߵĽ���ʽΪ��y=��x+3����x-1��=x2+2x-3��
��2������EG��x�ᣬ��E��G����ֱ��x=-1�Գƣ���G��-2��-3����
�辭����G�ġ�˫�����ߡ������ߵĽ���ʽΪ��y=kx+b��
����-2k+b=-3��b=2k-3��
��y=kx+2k-3��
����G��ͬʱ�����ߺ������ߵ�ͼ���ϣ�
����x2+2x-3=kx+2k-3��
��x2+��2-k��x-2k=0��
������������ֻ��һ�����㣬��
��=��2-k��2+8k=0��
���k=-2��
���������ߵĽ���ʽΪ��y=-2x-7��
| 1 |
| 2 |
��AP=2����A��-3��0����
����A��B���ڵ�P�Գƣ���B��1��0����
�辭��A��E��B�������ߵĽ���ʽΪ��y=a��x+3����x-1�������У�
a��0+3����0-1��=-3��a=1��
�����������ߵĽ���ʽΪ��y=��x+3����x-1��=x2+2x-3��
��2������EG��x�ᣬ��E��G����ֱ��x=-1�Գƣ���G��-2��-3����
�辭����G�ġ�˫�����ߡ������ߵĽ���ʽΪ��y=kx+b��
����-2k+b=-3��b=2k-3��
��y=kx+2k-3��
����G��ͬʱ�����ߺ������ߵ�ͼ���ϣ�
����x2+2x-3=kx+2k-3��
��x2+��2-k��x-2k=0��
������������ֻ��һ�����㣬��
��=��2-k��2+8k=0��
���k=-2��
���������ߵĽ���ʽΪ��y=-2x-7��
���������⿼���˶��κ������ۺ�֪ʶ���ص㿼���˶��κ����ĶԳ��ԡ����κ�������ʽ��ȷ��������ͼ����������Լ������б�ʽ����Ҫ֪ʶ���漰��֪ʶ��㣬�ѶȽϴ�

��ϰ��ϵ�д�
 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
�����Ŀ
���е��鷽ʽ�У����˲����ղ鷽ʽ���ǣ�������
| A������һ��ţ�̵����� |
| B��������������ѧ����������� |
| C�����麽��ɴ��ϸ���������� |
| D������������ѧ��ÿ����������ʱ�� |
���и����У���������֤�����⡰�κ�ż������8�����������Ǽ�����ķ����ǣ�������
| A��17 | B��16 | C��8 | D��4 |
����
+
+
+
=��������
| x-y |
| x+y |
| y-z |
| y+z |
| z-x |
| z+x |
| (x-y)(y-z)(z-x) |
| (x+y)(y+z)(z+x) |
| A��-1 | B��0 | C��1 | D��2 |
 ��ͼ��������ABCD�����Ϊ16����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���BD����һ��P��ʹPC+PE�ĺ���С���������СֵΪ
��ͼ��������ABCD�����Ϊ16����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���BD����һ��P��ʹPC+PE�ĺ���С���������СֵΪ �÷�֤��֤�����⡰��֪����ͼ��L1��L2��ƽ�У���֤����1�١�2����֤��ʱӦ����
�÷�֤��֤�����⡰��֪����ͼ��L1��L2��ƽ�У���֤����1�١�2����֤��ʱӦ����