题目内容
 如图,直线y=
如图,直线y=| 4 |
| 3 |
| k |
| x |
| 4 |
| 3 |
| 9 |
| 2 |
| k |
| x |
| AO |
| BC |
分析:欲求k,可由平移的坐标特点,求出双曲线上点的坐标,再代入双曲线函数式求解.
解答: 解:设点A的坐标为(a,
解:设点A的坐标为(a,
a),
∵
=2,
取OA的中点D,
∴点B相当于点D向右平移了
个单位,
∵点D的坐标为(
a,
a),
∴B点坐标为(
+
a,
a),
∵点A,B都在反比例函数y=
的图象上,
∴a×
a=
a×(
+
a),
解得a=3或0(0不合题意,舍去)
∴点A的坐标为(3,4),
∴k=12.
 解:设点A的坐标为(a,
解:设点A的坐标为(a,| 4 |
| 3 |
∵
| AO |
| BC |
取OA的中点D,
∴点B相当于点D向右平移了
| 9 |
| 2 |
∵点D的坐标为(
| 1 |
| 2 |
| 2 |
| 3 |
∴B点坐标为(
| 9 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
∵点A,B都在反比例函数y=
| k |
| x |
∴a×
| 4 |
| 3 |
| 2 |
| 3 |
| 9 |
| 2 |
| 1 |
| 2 |
解得a=3或0(0不合题意,舍去)
∴点A的坐标为(3,4),
∴k=12.
点评:本题结合图形的平移考查反比例函数的性质及相似形的有关知识.平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.本题关键是利用了对应线段平行且相等的性质.

练习册系列答案
相关题目
 在,请说明理由;
在,请说明理由;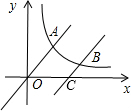 如图,直线y=
如图,直线y=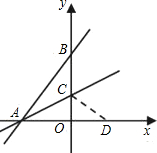 如图,直线y=
如图,直线y=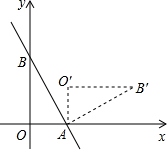 如图,直线y=-
如图,直线y=-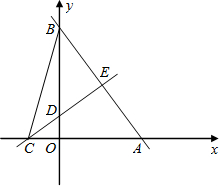 (2012•营口)如图,直线
(2012•营口)如图,直线