题目内容
 如图,在⊙O中,AB为弦,且AB⊥OP于D,PA为⊙O的切线,AB=8cm,OD=3cm,则PA的长为
如图,在⊙O中,AB为弦,且AB⊥OP于D,PA为⊙O的切线,AB=8cm,OD=3cm,则PA的长为考点:切线的性质
专题:
分析:在直角△AOD中,利用勾股定理求得OA的长,然后证明△APD∽△OAD,根据相似三角形的对应边的比相等即可求解.
解答:解:∵AB⊥OP,
∴AD=
AB=
×8=4cm,
在直角△ADO中,OA=
=
=5,
∵PA为⊙O的切线,
∴∠PAO=90°,即∠PAD+∠OAD=90°,
又∵直角△AOD中,∠OAD+∠AOD=90°,
∴∠AOD=∠PAD,
又∵∠ADP=∠ADO,
∴△APD∽△OAD,
∴
=
,即
=
,
解得:PA=
(cm).
故答案是:
cm.
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
在直角△ADO中,OA=
| AD2+OD2 |
| 42+32 |
∵PA为⊙O的切线,
∴∠PAO=90°,即∠PAD+∠OAD=90°,
又∵直角△AOD中,∠OAD+∠AOD=90°,
∴∠AOD=∠PAD,
又∵∠ADP=∠ADO,
∴△APD∽△OAD,
∴
| PA |
| OA |
| AD |
| OD |
| PA |
| 5 |
| 4 |
| 3 |
解得:PA=
| 20 |
| 3 |
故答案是:
| 20 |
| 3 |
点评:本题考查了勾股定理,切线的性质以及相似三角形的判定与性质,证明△APD∽△OAD是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若△ABC≌△DEF,点A和D,点B和E是对应顶点,∠A=80°,∠B=40°,那么∠F的度数是( )
| A、80° | B、40° |
| C、60° | D、120° |
 如图,已知S△ABC=S△ABD,求证:AB∥CD.
如图,已知S△ABC=S△ABD,求证:AB∥CD. 已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD.
已知,△ABC内接于⊙O,AB=BC,∠BAC平分线交于⊙O于点P,自P点作PD⊥AB,垂足为D,求证:AB-AC=2BD. 若用A、B、C、分别表示有理数a、b、c,0为原点,如图所示.已知a<c<0,b>0.
若用A、B、C、分别表示有理数a、b、c,0为原点,如图所示.已知a<c<0,b>0.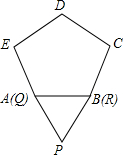 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为