Question

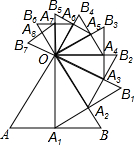已知等边三角形AOB的边长为32，以AB边上的高OA₁为边按顺时针方向做等边三角形OA₂B₂，与OB相交于A₂，如图，按此做法进行下去．
（1）求线段OA₁，OA₂的长度；
（2）写出OA₃，OA₄，OA₅的长，你能用一句话或一个等式描述各三角形边长之间的关系吗？
（3）用你发现的规律，求△OA₆B₆的周长和面积．

Answer 1

分析：（1）由等边三角形AOB的边长为32，以AB边上的高OA₁为边按顺时针方向做等边三角形OA₂B₂，与OB相交于A₂，根据等边三角形的性质，可求得OA₁的长，同理可求得OA₂的长度；
（2）由（1）可求得OA₃，OA₄，OA₅的长，即可得到规律：边长的关系OA_n=

3

2

OA_n-1；
（3）由规律，可求得OA₆的长，则可求得△OA₆B₆的周长，继而求得OA₇的长，则可求得△OA₆B₆的面积．

解答：解：（1）∵△AOB是等边三角形，OA₁为高，
∴∠A=60°，AA₁=

1

2

AB=16，
∴OA₁=

OA2-AA12

=16

3

；
同理：OA₂=24；

（2）同理：OA₃=12

3

，OA₄=18，OA₅=9

3

；
∴边长的关系OA_n=

3

2

OA_n-1；

（3）∵OA₆=

3

2

OA₅=

27

2

，
∴周长：

81

2

；
∵OA₇=

3

2

OA₆=

27 3

4

，
∴面积：

1

2

×

27

2

×

27 3

4

=

729 3

16

．

点评：此题考查了等边三角形的性质以及勾股定理．此题属于规律性题目，注意得到规律：边长的关系OA_n=

3

2

OA_n-1是解此题的关键．