题目内容
如图,等腰梯形ABCD中,AD∥BC,∠B=450,P是BC边上一点,△PAD的面积为 ,设AB=x,AD=y。
,设AB=x,AD=y。

(1)求y与x的函数关系式;
(2)若∠APD=450,当y=1时,求PB·PC的值;
(3)若∠APD=900,求y的最小值。
 ,设AB=x,AD=y。
,设AB=x,AD=y。
(1)求y与x的函数关系式;
(2)若∠APD=450,当y=1时,求PB·PC的值;
(3)若∠APD=900,求y的最小值。
(1) (2)2(3)
(2)2(3)
 (2)2(3)
(2)2(3)
解:(1)如图,过点A作AE⊥BC于点E,

∵AB=x,∠B=450,∴ 。
。
又∵AD=y,△PAD的面积为 ,
,
∴ ,即
,即 。
。
∴y与x的函数关系式为 。
。
(2)∵四边形ABCD是等腰梯形, AD=y=1,∴∠B=∠C,AB=DC= 。
。
∵∠B+∠1+∠4=1800,∠1+∠2+∠3=1800,
∴∠B+∠4=∠2+∠3。
∵∠B=450,∠2=∠APD=450,∴∠4=∠3。
∴△BPA∽△CDP。∴ 。
。
∴ 。
。

(3)如图,过AD的中点为圆心, AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,

∵AD∥BC,∴四边形AEFO是矩形。
∴ 。
。
又OP=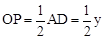 ,设PF=t,则
,设PF=t,则 ,即
,即 。
。
设 ,则
,则 ,
, (负值舍去)。
(负值舍去)。
∴根据偶次幂和算术平方根的非负性质,当 时,
时, 最小,最小值为2。
最小,最小值为2。
∴ 的最小值为
的最小值为 。
。
(1)依题设,根据等腰梯形的性质,用x表示出△PAD的AD边上的高,即可由△PAD的面积
为 列式得到y与x的函数关系式。
列式得到y与x的函数关系式。
(2)证明△BPA∽△CDP即可得到PB·PC的值。
(3)由∠APD=900,根据直径所对圆周角是直角的性质,过AD的中点为圆心, AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得 ,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。
,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。

∵AB=x,∠B=450,∴
 。
。又∵AD=y,△PAD的面积为
 ,
,∴
 ,即
,即 。
。∴y与x的函数关系式为
 。
。(2)∵四边形ABCD是等腰梯形, AD=y=1,∴∠B=∠C,AB=DC=
 。
。∵∠B+∠1+∠4=1800,∠1+∠2+∠3=1800,
∴∠B+∠4=∠2+∠3。
∵∠B=450,∠2=∠APD=450,∴∠4=∠3。
∴△BPA∽△CDP。∴
 。
。∴
 。
。
(3)如图,过AD的中点为圆心,
 AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,
∵AD∥BC,∴四边形AEFO是矩形。
∴
 。
。又OP=
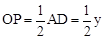 ,设PF=t,则
,设PF=t,则 ,即
,即 。
。设
 ,则
,则 ,
, (负值舍去)。
(负值舍去)。∴根据偶次幂和算术平方根的非负性质,当
 时,
时, 最小,最小值为2。
最小,最小值为2。∴
 的最小值为
的最小值为 。
。(1)依题设,根据等腰梯形的性质,用x表示出△PAD的AD边上的高,即可由△PAD的面积
为
 列式得到y与x的函数关系式。
列式得到y与x的函数关系式。(2)证明△BPA∽△CDP即可得到PB·PC的值。
(3)由∠APD=900,根据直径所对圆周角是直角的性质,过AD的中点为圆心,
 AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得
AD为半径画圆,交BC于点P,则∠APD=900,连接OP,过点O作OF⊥BC于点F,设PF=t,应用勾股定理得 ,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。
,化简,解方程,根据偶次幂和算术平方根的非负性质,求得结果。
练习册系列答案
相关题目
 ,高DF= .
,高DF= .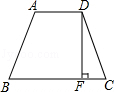
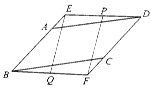
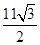
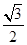




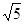 时,四边形BA′CD为等腰梯形;
时,四边形BA′CD为等腰梯形;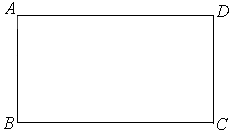

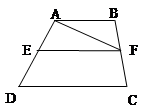
 倍,则这个多边形的边数是
倍,则这个多边形的边数是