题目内容
如图,等腰梯形ABCD中,AD∥BC,若AB=AD=4,BC=8,以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外,则半径r的范围是______.
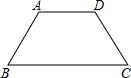

连接AC作AE⊥BC于点E,
∵等腰梯形ABCD中,AD∥BC,AB=AD=4,BC=8,
∴BE=2,
∴cos∠B=
=
,
∴∠B=60°,
∴∠BCD=60°,
∴∠BAD=∠D=120°,
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴AC=
=
=4
,
当以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外时,
半径r的范围是:4≤r<4
.
故答案为:4≤r<4
.

∵等腰梯形ABCD中,AD∥BC,AB=AD=4,BC=8,
∴BE=2,
∴cos∠B=
| BE |
| AB |
| 1 |
| 2 |
∴∠B=60°,
∴∠BCD=60°,
∴∠BAD=∠D=120°,
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴AC=
| BC2-AB2 |
| 64-16 |
| 3 |
当以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外时,
半径r的范围是:4≤r<4
| 3 |
故答案为:4≤r<4
| 3 |


练习册系列答案
相关题目




