题目内容
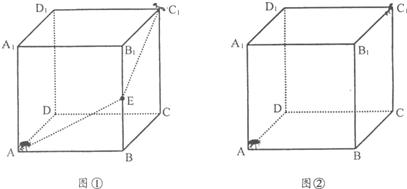
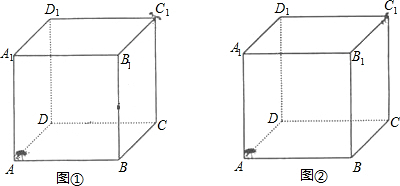
 如图,有一只棱长为20厘米的正方形盒子,一只蚂蚁从A点出发,沿着正方体木箱的外表面爬行到CD的中点P的最短路线长为
如图,有一只棱长为20厘米的正方形盒子,一只蚂蚁从A点出发,沿着正方体木箱的外表面爬行到CD的中点P的最短路线长为
- A.10
 厘米
厘米 - B.50厘米
- C.10
 厘米
厘米 - D.30厘米
C
分析:把此正方体的ADD′A′面与CDD′C′面展开在同一平面内,形成矩形AA′C′C,然后利用勾股定理求点A和P点间的线段长,即可得到蚂蚁爬行的最短距离.
解答:把正方体的ADD′A′面与CDD′C′面展开在同一平面内,
在矩形AA′C′C中
∵P为C′D′的中点,两点之间线段最短,
∴A′P=30,
在Rt△AA′P中,AP= =10
=10 厘米.
厘米.
故选C.
点评:考查了平面展开-最短路径问题,化空间问题为平面问题是解决空间几何体问题的主要思想,本题“化曲面为平面”解决了“怎样爬行最近”问题.
分析:把此正方体的ADD′A′面与CDD′C′面展开在同一平面内,形成矩形AA′C′C,然后利用勾股定理求点A和P点间的线段长,即可得到蚂蚁爬行的最短距离.
解答:把正方体的ADD′A′面与CDD′C′面展开在同一平面内,
在矩形AA′C′C中
∵P为C′D′的中点,两点之间线段最短,
∴A′P=30,
在Rt△AA′P中,AP=
 =10
=10 厘米.
厘米.故选C.
点评:考查了平面展开-最短路径问题,化空间问题为平面问题是解决空间几何体问题的主要思想,本题“化曲面为平面”解决了“怎样爬行最近”问题.

练习册系列答案
相关题目
 如图,有一只棱长为20厘米的正方形盒子,一只蚂蚁从A点出发,沿着正方体木箱的外表面爬行到CD的中点P的最短路线长为( )
如图,有一只棱长为20厘米的正方形盒子,一只蚂蚁从A点出发,沿着正方体木箱的外表面爬行到CD的中点P的最短路线长为( )A、10
| ||
| B、50厘米 | ||
C、10
| ||
| D、30厘米 |

 厘米
厘米 厘米
厘米