题目内容
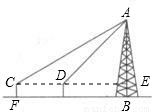
 如图,为了测量电视塔AB的高度,在C、D两点测得塔顶A的仰角分别为30°,45°.已知C、D两点在同一水平线上,C、D间的距离为60米,测倾器CF的高为1.5米,求电视塔AB的高.(精确到0.1米)
如图,为了测量电视塔AB的高度,在C、D两点测得塔顶A的仰角分别为30°,45°.已知C、D两点在同一水平线上,C、D间的距离为60米,测倾器CF的高为1.5米,求电视塔AB的高.(精确到0.1米)
分析:根据AE和∠ADE、AE和∠ACE可以求得DE、CE的长度,根据CD=CE-DE可以求出AE的长度,即可解题.
解答:解:在Rt△ADE中,DE=
=AE,
Rt△ACE中,CE=
=
AE,
∵CD=CE-DE,
∴AE=
=30(
+1)米=81.96米
所以电视塔高为81.96米+1.5米=83.46米≈83.5米.
答:电视塔AB的高约83.5米.
| AE |
| tan45° |
Rt△ACE中,CE=
| AE |
| tan30° |
| 3 |
∵CD=CE-DE,
∴AE=
| CD | ||
|
| 3 |
所以电视塔高为81.96米+1.5米=83.46米≈83.5米.
答:电视塔AB的高约83.5米.
点评:本题考查了特殊角的三角函数值,考查了三角函数在直角三角形中的应用,本题中求DE、CE的长度是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
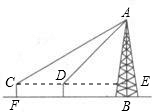
 91、如图,为了测量某电视塔的高度,在离电阻墙202m的D处,用测角仪测得塔顶A的仰角为47°,已知测角仪的高CD=1.4m,则电视塔的高度AB为
91、如图,为了测量某电视塔的高度,在离电阻墙202m的D处,用测角仪测得塔顶A的仰角为47°,已知测角仪的高CD=1.4m,则电视塔的高度AB为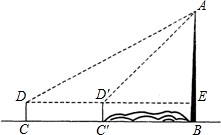 如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度(
如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度(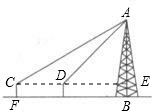 如图,为了测量电视塔AB的高度,在C、D两点测得塔顶A的仰角分别为30°,45°.已知C、D两点在同一水平线上,C、D间的距离为60米,测倾器CF的高为1.5米,求电视塔AB的高.(精确到0.1米)
如图,为了测量电视塔AB的高度,在C、D两点测得塔顶A的仰角分别为30°,45°.已知C、D两点在同一水平线上,C、D间的距离为60米,测倾器CF的高为1.5米,求电视塔AB的高.(精确到0.1米)