题目内容
【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=![]() .
.
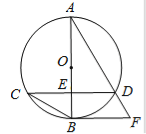
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长.
【答案】(1)见解析(2)2(3)![]()
【解析】解:(1)∵BF是⊙O的切线 ∴AB⊥BF …………………1分
∵AB⊥CD
∴CD∥BF………………………………………………2分
(2)连结BD
∵AB是直径 ∴∠ADB=90° ………………………………………3分
∵∠BCD=∠BAD cos∠BCD=![]() …………………4分
…………………4分
∴cos∠BAD=![]()
又∵AD=3 ∴AB=4
∴⊙O的半径为2 ……………………………………5分
(3)∵cos∠DAE=![]() AD=3∴AE=
AD=3∴AE=![]() …………………………6分
…………………………6分
∴ED= ……………………………………………7分
……………………………………………7分
∴CD=2ED=![]() ………………………………………………………8分
………………………………………………………8分
(1)由平行公理可得
(2)连结BD,利用三角函数求得![]() 通过已知,即可求得⊙O的半径
通过已知,即可求得⊙O的半径
(3)利用三角函数求得AE的长,通过勾股定理求得ED的长,从而求得弦CD的长

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目