题目内容
如图,在平面直角坐标中,边长为2的正方形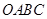 的两顶点
的两顶点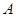 、
、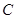 分别在
分别在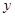 轴、
轴、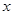 轴的正半轴上,点
轴的正半轴上,点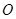 在原点.现将正方形
在原点.现将正方形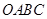 绕
绕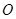 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当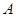 点第一次落在直线
点第一次落在直线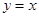 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中, 边交直线
边交直线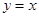 于点
于点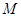 ,
,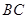 边交
边交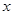 轴于点
轴于点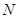 .
.
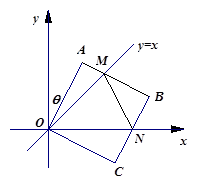
(1)当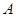 点第一次落在直线
点第一次落在直线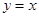 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);
(2)设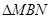 的周长为
的周长为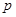 ,在旋转正方形
,在旋转正方形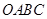 的过程中,
的过程中,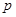 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
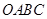 的两顶点
的两顶点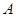 、
、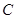 分别在
分别在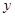 轴、
轴、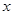 轴的正半轴上,点
轴的正半轴上,点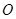 在原点.现将正方形
在原点.现将正方形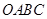 绕
绕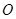 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当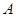 点第一次落在直线
点第一次落在直线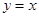 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中, 边交直线
边交直线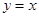 于点
于点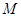 ,
,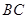 边交
边交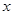 轴于点
轴于点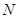 .
.
(1)当
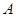 点第一次落在直线
点第一次落在直线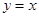 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);(2)设
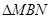 的周长为
的周长为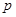 ,在旋转正方形
,在旋转正方形 的过程中,
的过程中,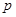 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.(1) A点坐标为( ,
, ),B点坐标为(2
),B点坐标为(2 ,0) 4分
,0) 4分
(2)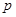 值无变化. 证明 见解析 5分
值无变化. 证明 见解析 5分
 ,
, ),B点坐标为(2
),B点坐标为(2 ,0) 4分
,0) 4分(2)
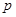 值无变化. 证明 见解析 5分
值无变化. 证明 见解析 5分(1)根据勾股定理求得两点的坐标;
(2)延长BA交y轴于E点,可以证明:△OAE≌△OCN,△OME≌△OMN证得:OE=ON,AE=CN,MN=ME=AM+AE=AM+CN.
从而求得:P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.即可求解.
证明:延长 交
交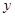 轴于
轴于 点.在
点.在 中
中
 ∴
∴
∴ . 7分
. 7分
在 中
中
 ∴
∴ .
.
∴ ∴
∴ 8分
8分
∴ . 10分
. 10分
(2)延长BA交y轴于E点,可以证明:△OAE≌△OCN,△OME≌△OMN证得:OE=ON,AE=CN,MN=ME=AM+AE=AM+CN.
从而求得:P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.即可求解.
证明:延长
 交
交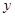 轴于
轴于 点.在
点.在 中
中 ∴
∴
∴
 . 7分
. 7分在
 中
中 ∴
∴ .
.∴
 ∴
∴ 8分
8分∴
 . 10分
. 10分
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目



 ,则此直线与两坐标轴围成的三角形的面积为
,则此直线与两坐标轴围成的三角形的面积为 


 .
.
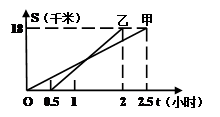

 ,L
,L 分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题: