题目内容
α,β为关于x的一元二次方程x2- x+2=0的两个根,则代数式2α2+β2+
x+2=0的两个根,则代数式2α2+β2+ β-3的值为________.
β-3的值为________.
11
分析:由根与系数的关系可知:α+β= ,α•β=2,而2α2+β2+
,α•β=2,而2α2+β2+ β-3=2α2+β2+(α+β)β-3=2(α2+β2)+αβ-3=2(α+β)2-3αβ-3,然后把前面的值代入即可求出其值.
β-3=2α2+β2+(α+β)β-3=2(α2+β2)+αβ-3=2(α+β)2-3αβ-3,然后把前面的值代入即可求出其值.
解答:由根与系数的关系可知:
α+β= ,α•β=2,
,α•β=2,
而2α2+β2+ β-3
β-3
=2α2+β2+(α+β)β-3
=2(α2+β2)+αβ-3
=2(α+β)2-3αβ-3
=2×10-3×2-3
=11.
故填空答案:11.
点评:灵活运用根与系数的关系是解决本题的关键,特别是α+β= 这个式子的转换.
这个式子的转换.
分析:由根与系数的关系可知:α+β=
 ,α•β=2,而2α2+β2+
,α•β=2,而2α2+β2+ β-3=2α2+β2+(α+β)β-3=2(α2+β2)+αβ-3=2(α+β)2-3αβ-3,然后把前面的值代入即可求出其值.
β-3=2α2+β2+(α+β)β-3=2(α2+β2)+αβ-3=2(α+β)2-3αβ-3,然后把前面的值代入即可求出其值.解答:由根与系数的关系可知:
α+β=
 ,α•β=2,
,α•β=2,而2α2+β2+
 β-3
β-3=2α2+β2+(α+β)β-3
=2(α2+β2)+αβ-3
=2(α+β)2-3αβ-3
=2×10-3×2-3
=11.
故填空答案:11.
点评:灵活运用根与系数的关系是解决本题的关键,特别是α+β=
 这个式子的转换.
这个式子的转换. 
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
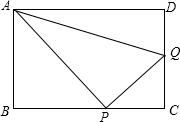
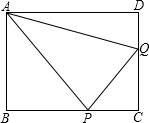 t=2时,P、Q两点恰好同时到达目的地.
t=2时,P、Q两点恰好同时到达目的地.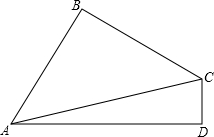 两根.
两根. 已知△ABC的一边AC为关于x的一元二次方程x2+mx+5=0的两个正整数根之一,且另两边长为BC=3,AB=5,求cosA.
已知△ABC的一边AC为关于x的一元二次方程x2+mx+5=0的两个正整数根之一,且另两边长为BC=3,AB=5,求cosA.