题目内容
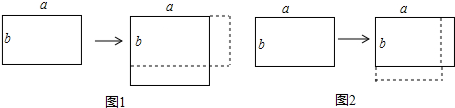
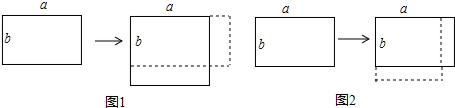
一块原边长分别为a,b(a>1,b>1)的长方形,一边增加1,另一边减少1.
(1)当a=b时,变化后的面积是增加还是减少?
(2)当a>b时,有两种方案,第一种方案如图1,第二种方案如图2.请你比较这两种方案,确定哪一种方案变化后的面积比较大.
解:(1)设原来长方形的面积是S1,变化后的长方形的面积是S2,
根据题意得:S =ab,S2=(a+1)(b-1)=ab+b-a-1,
=ab,S2=(a+1)(b-1)=ab+b-a-1,
∴S2-S1=ab+b-a-1-ab=b-a-1,
∵a=b,
∴b-a-1=-1<0,
∴S2<S1,
∴变化后面积减小了.
(2)方案1,S1=(a+1)(b-1)=ab-a+b-1,
方案2,S2=(a-1)(b+1)=ab+a-b-1,
∴S1-S2=-2a+2b=-2(a-b),
∵a>b,
∴S1-S2<0,
∴方案2变化后面积大.
分析:(1)根据题意得出算式,求出两式的差,再判断即可;
(2)求出两种方案的算式,求出两式的差,再判断即可.
点评:本题考查了整式的混合运算的应用,关键是能根据题意列出算式.
根据题意得:S
 =ab,S2=(a+1)(b-1)=ab+b-a-1,
=ab,S2=(a+1)(b-1)=ab+b-a-1,∴S2-S1=ab+b-a-1-ab=b-a-1,
∵a=b,
∴b-a-1=-1<0,
∴S2<S1,
∴变化后面积减小了.
(2)方案1,S1=(a+1)(b-1)=ab-a+b-1,
方案2,S2=(a-1)(b+1)=ab+a-b-1,
∴S1-S2=-2a+2b=-2(a-b),
∵a>b,
∴S1-S2<0,
∴方案2变化后面积大.
分析:(1)根据题意得出算式,求出两式的差,再判断即可;
(2)求出两种方案的算式,求出两式的差,再判断即可.
点评:本题考查了整式的混合运算的应用,关键是能根据题意列出算式.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
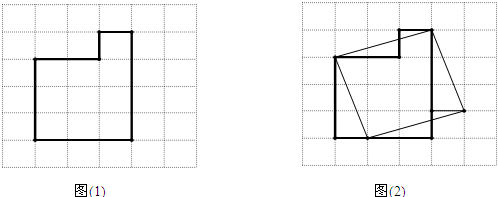

 .由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长.于是,画出如图(2)所示的正方形.
.由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长.于是,画出如图(2)所示的正方形.
 .由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长.于是,画出如图(2)所示的正方形.
.由此可知正方形的边长等于两个直角边分别为30cm和10cm的直角三角形斜边的长.于是,画出如图(2)所示的正方形.