题目内容
抛物线y=x2-x-2与坐标轴交点为点A、B、C，则△ABC的面积为________．
3
分析：先根据抛物线y=x2-x-2找到与坐标轴的三个交点，则该三角形的面积可求．
解答：解方程x2-x-2=0，
∴x1=2，x2=-1，
∴它与x轴的三个交点分别是：（-1，0），（2，0）；
当x=0时，y=-2，
∴它与y轴的交点是：（0，-2）
∴该三角形的面积为
×2×3=3．
故答案为：3．
点评：本题考查了抛物线与坐标轴的交点求法，解决此问题的关键是正确求出抛物线与坐标轴的交点坐标．
分析：先根据抛物线y=x2-x-2找到与坐标轴的三个交点，则该三角形的面积可求．
解答：解方程x2-x-2=0，
∴x1=2，x2=-1，
∴它与x轴的三个交点分别是：（-1，0），（2，0）；
当x=0时，y=-2，
∴它与y轴的交点是：（0，-2）
∴该三角形的面积为
×2×3=3．故答案为：3．
点评：本题考查了抛物线与坐标轴的交点求法，解决此问题的关键是正确求出抛物线与坐标轴的交点坐标．
练习册系列答案
相关题目
A是抛物线与x轴的另一个交点．
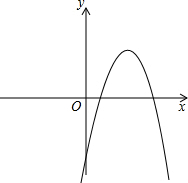已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是