题目内容
1.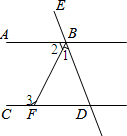 如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,求证:BA平分∠EBF.
如图,已知AB∥CD,∠1:∠2:∠3=1:2:3,求证:BA平分∠EBF.
分析 首先根据两直线平行,同旁内角互补可得∠2+∠3=180°,再设∠1=x°,∠2=2x°,∠3=3x°,根据∠2+∠3=180°可得2x+3x=180,解出x的值,然后可得∠2,∠EBA的度数,进而可得BA平分∠EBF.
解答 证明:∵AB∥CD,
∴∠2+∠3=180°,
∵∠1:∠2:∠3=1:2:3,
∴设∠1=x°,∠2=2x°,∠3=3x°,
∴2x+3x=180,
解得:x=36,
∴∠1=36°,∠2=72°,
∴∠EBA=180°-36°-72°=72°,
∴BA平分∠EBF.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补,以及方程思想的应用.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
11.如果一组数据5,-2,0,6,4,x的平均数为3,那么x等于( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
16.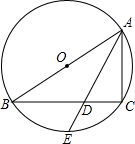 如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于E,交BC于D.若⊙O的半径为5,AC=6,那么DE的长为( )
如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于E,交BC于D.若⊙O的半径为5,AC=6,那么DE的长为( )
 如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于E,交BC于D.若⊙O的半径为5,AC=6,那么DE的长为( )
如图,AB是⊙O的直径,点C在⊙O上,∠BAC的平分线交⊙O于E,交BC于D.若⊙O的半径为5,AC=6,那么DE的长为( )| A. | $\frac{9}{5}$$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
6.下列命题中,真命题的个数有( )
①同一平面内,两条直线一定互相平行;
②有一条公共边的角叫邻补角;
③对顶角相等;
④内错角相等;
⑤无理数都是无限小数;
⑥从直线外一点到这条直线的垂线段,叫做点到直线的距离.
①同一平面内,两条直线一定互相平行;
②有一条公共边的角叫邻补角;
③对顶角相等;
④内错角相等;
⑤无理数都是无限小数;
⑥从直线外一点到这条直线的垂线段,叫做点到直线的距离.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列式子,一定成立的是( )
| A. | 32=6 | B. | -32=9 | C. | |-23|=8 | D. | (-1)8=-1 |
11.下列命题中,逆命题是真命题的是( )
| A. | 两直线平行,内错角相等 | |
| B. | 如果两个角都是直角,那么他们相等 | |
| C. | 全等三角形对应角都相等 | |
| D. | 如果x=1,那么|x|=1 |
 如图,已知∠1=100°,∠2=80°,∠3=105°,则∠4=85°.
如图,已知∠1=100°,∠2=80°,∠3=105°,则∠4=85°. 已知:如图,∠B+∠A=180°,则AD∥BC,理由是同旁内角互补,两直线平行;
已知:如图,∠B+∠A=180°,则AD∥BC,理由是同旁内角互补,两直线平行;