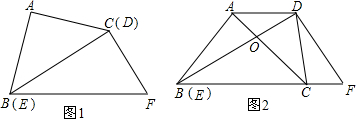题目内容
（2013•威海）将一副直角三角板如图摆放，点C在EF上，AC经过点D．已知∠A=∠EDF=90°，AB=AC．∠E=30°，∠BCE=40°，则∠CDF=25°
25°
．分析：由∠A=∠EDF=90°，AB=AC．∠E=30°，∠BCE=40°，可求得∠ACE的度数，又由三角形外角的性质，可得∠CDF=∠ACE-∠F=∠BCE+∠ACB-∠F，继而求得答案．
解答：解：∵AB=AC，∠A=90°，
∴∠ACB=∠B=45°，
∵∠EDF=90°，∠E=30°，
∴∠F=90°-∠E=60°，
∵∠ACE=∠CDF+∠F，∠BCE=40°，
∴∠CDF=∠ACE-∠F=∠BCE+∠ACB-∠F=45°+40°-60°=25°．
故答案为：25°．
∴∠ACB=∠B=45°，
∵∠EDF=90°，∠E=30°，
∴∠F=90°-∠E=60°，
∵∠ACE=∠CDF+∠F，∠BCE=40°，
∴∠CDF=∠ACE-∠F=∠BCE+∠ACB-∠F=45°+40°-60°=25°．
故答案为：25°．
点评：本题考查三角形外角的性质以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
（2013•威海）如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（ ）
