题目内容
解方程: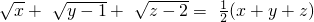 .
.
解:将原方程变形为:
x+y+z-2 -2
-2 -2
-2 =0,
=0,
∴(x-2 +1)+(y-1-2
+1)+(y-1-2 +1)+(z-2-2
+1)+(z-2-2 +1)=0,
+1)=0,
配方得: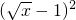 +
+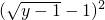 +
+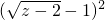 =0,
=0,
利用非负数的性质得 =1,
=1, =1,
=1, =1,
=1,
所以x=1,y=2,z=3.
经检验,x=1,y=2,z=3是原方程的根,
所以原方程的根为:x=1,y=2,z=3.
分析:三个未知量、一个方程,要有确定的解,则方程的结构必然是极其特殊的.将原方程变形为x+y+z-2 -2
-2 -2
-2 =0,
=0,
先配方后根据非负数的性质即可求解.
点评:本题考查了无理方程,难度较大,关键是将原方程正确的变形后构造成几个非负数的平方之和为0的形式.
x+y+z-2
 -2
-2 -2
-2 =0,
=0,∴(x-2
 +1)+(y-1-2
+1)+(y-1-2 +1)+(z-2-2
+1)+(z-2-2 +1)=0,
+1)=0,配方得:
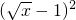 +
+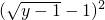 +
+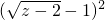 =0,
=0,利用非负数的性质得
 =1,
=1, =1,
=1, =1,
=1,所以x=1,y=2,z=3.
经检验,x=1,y=2,z=3是原方程的根,
所以原方程的根为:x=1,y=2,z=3.
分析:三个未知量、一个方程,要有确定的解,则方程的结构必然是极其特殊的.将原方程变形为x+y+z-2
 -2
-2 -2
-2 =0,
=0,先配方后根据非负数的性质即可求解.
点评:本题考查了无理方程,难度较大,关键是将原方程正确的变形后构造成几个非负数的平方之和为0的形式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目