Question

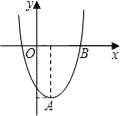
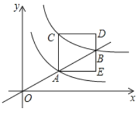
【题目】如图，过原点的直线与反比例函数y=（x>0）、反比例函数y=（x>0）的图象分别交于A、B两点，过点A作y轴的平行线交反比例函数y=（x>0）的图象于C点，以AC为边在直线AC的右侧作正方形ACDE，点B恰好在边DE上，则正方形ACDE的面积为______．

Answer 1

【答案】4-4

【解析】

设直线AB的解析式为y=kx，A（m，），B（n，），则C（m，），根据直线的解析式求得k==，进而求得n=，根据AC=AE，求得=-1，因为S正方形=AC2=（）2，即可求得正方形ACDE的面积.

设直线AB的解析式为y=kx，A（m，），B（n，），C（m，），
∴，
∴k==，
∴n=m，
∵AC=AE，即=n-m，
∴=m-m，，解得：=-1，
∵S正方形=AC2=（）2=4×=4（-1）=4-4.