题目内容
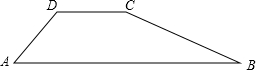
某水库大坝横断面是梯形ABCD ,坝顶宽CD=3米,斜坡AD=16米,坝高8米,斜坡BC的坡度 =1∶3,求斜坡AD的坡角和坝底宽AB。
=1∶3,求斜坡AD的坡角和坝底宽AB。
 =1∶3,求斜坡AD的坡角和坝底宽AB。
=1∶3,求斜坡AD的坡角和坝底宽AB。
解:作DE⊥AB,CF⊥AB,垂足分别为E 、F,
在Rt △ADE 和Rt △BCF 中
∵
∴∠A=30°
又∵ ,
,
∴BF=3CF=3×8=24
∴AB=AE+EF+BF
=
= (米)
(米)
答:斜坡AD的坡角∠A=300,坝底宽AB为 米。
米。
在Rt △ADE 和Rt △BCF 中
∵

∴∠A=30°
又∵
 ,
,
∴BF=3CF=3×8=24
∴AB=AE+EF+BF
=

=
 (米)
(米)答:斜坡AD的坡角∠A=300,坝底宽AB为
 米。
米。
练习册系列答案
相关题目