题目内容
如图，梯形ABCD中，AB∥CD，∠ADC+∠BCD=90°，以AD、AB、BC为斜边向外作等腰直角三角形，其面积分别为S1，S2，S3，且S1+S3=4S2，若将梯形上底AB沿BC方向平移至下底CD上的CE处，连AE，则下列结论：①AE∥BC；②AE=BC；③
| AB |
| DC |
| 1 |
| 2 |
| DC2-AD2-BC2 |
| AB2 |
其中正确的结论的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：梯形,勾股定理,等腰直角三角形
专题：
分析：①由平移的性质，即可得AE∥BC；
②易得四边形ABCE是平行四边形，则可得AE=BC；
③分别用斜边AD、AB、BC把S1、S2、S3表示出来，然后根据S1+S3=4S2求出AD、AB、BC之间的关系．可得△ADE是直角三角形，利用勾股定理即可发现CD和AB之间的关系．
④由③即可求得
=5．
②易得四边形ABCE是平行四边形，则可得AE=BC；
③分别用斜边AD、AB、BC把S1、S2、S3表示出来，然后根据S1+S3=4S2求出AD、AB、BC之间的关系．可得△ADE是直角三角形，利用勾股定理即可发现CD和AB之间的关系．
④由③即可求得
| DC2-AD2-BC2 |
| AB2 |
解答：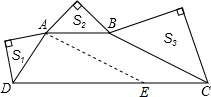
解：①如图，根据平移的性质，可得AE∥BC，故①正确；
②∵AB∥CD，AE∥BC，
∴四边形ABCE是平行四边形，
∴AE=BC，故②正确；
③解：∵以AD、AB、BC为斜边向外作等腰直角三角形，其面积分别是S1、S2、S3，
∴S1=
，S2=
，S3=
，
∵S1+S3=4S2，
∴AD2+BC2=4AB2，
∵AE=BC，EC=AB，
∵∠ADC+∠BCD=90°，
∴∠ADC+∠AED=90°，
∴AD2+AE2=DE2，
∴AD2+BC2=DE2，
∴DE2=4AB2，
∴DE=2AB，
∴CD=3AB．
∴
=
，故③错误；
④∵AD2+BC2=4AB2，CD=3AB，
∴
=
=5．
故④正确．
故选C．
解：①如图，根据平移的性质，可得AE∥BC，故①正确；②∵AB∥CD，AE∥BC，
∴四边形ABCE是平行四边形，
∴AE=BC，故②正确；
③解：∵以AD、AB、BC为斜边向外作等腰直角三角形，其面积分别是S1、S2、S3，
∴S1=
| AD2 |
| 4 |
| AB2 |
| 4 |
| BC2 |
| 4 |
∵S1+S3=4S2，
∴AD2+BC2=4AB2，
∵AE=BC，EC=AB，
∵∠ADC+∠BCD=90°，
∴∠ADC+∠AED=90°，
∴AD2+AE2=DE2，
∴AD2+BC2=DE2，
∴DE2=4AB2，
∴DE=2AB，
∴CD=3AB．
∴
| AB |
| DC |
| 1 |
| 3 |
④∵AD2+BC2=4AB2，CD=3AB，
∴
| DC2-AD2-BC2 |
| AB2 |
| 9AB2-4AB2 |
| AB2 |
故④正确．
故选C．
点评：此题考查了梯形的性质、平行四边形的判定与性质、勾股定理以及等腰直角三角形的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
能使二元一次方程2x-y=6左、右两边的值相等的一对数值是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，直角梯形MNPQ，∠MNP=90°，PM⊥NQ，若| NQ |
| PM |
| ||
| 2 |
| MQ |
| NP |
A、
| ||||
B、
| ||||
| C、4 | ||||
D、
|
