题目内容
(2009•房山区一模)已知:二次函数y=ax2-x+c的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x= ,且图象向右平移一个单位后经过坐标原点O.
,且图象向右平移一个单位后经过坐标原点O.(1)求这个二次函数的解析式;
(2)求△ABC的外接圆圆心D的坐标及⊙D的半径;
(3)设⊙D的面积为S,在抛物线上是否存在点M,使得S△ACM=
 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】分析:(1)依题意可推出抛物线对称轴是直线x= ,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;
,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;
(2)作线段BC和线段AB的垂直平分线,它们的交点就是圆心D,根据点的坐标特点即抛物线的对称轴可求,用勾股定理求半径;
(3)根据(2)可求S=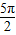 ,故S△ACM=
,故S△ACM=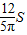 =6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.
=6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.
解答: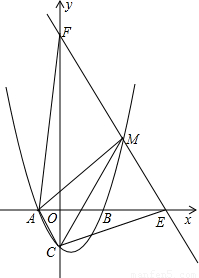 解:(1)∵抛物线的对称轴是直线x=
解:(1)∵抛物线的对称轴是直线x=
∴-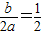
∴a=1,(1分)
∵抛物线向右平移一个单位过坐标原点(0,0),
∴原抛物线过点(-1,0)
∴c=-2
∴抛物线的解析式为y=x2-x-2(2分)
(2)∵OC=OB=2,线段BC的垂直平分线为直线y=-x
∵抛物线的对称轴为直线x=
∴△ABC外接圆⊙D的圆心D( ,-
,- )(3分)
)(3分)
∵∠ABC=45°,
∴∠ADC=90°
∵AC=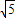 ,
,
∴AD=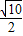 ,
,
即△ABC外接圆半径为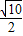 (4分)
(4分)
(3)∵S=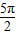 ,
,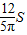 =6,
=6,
∴S△ACM=6(5分)
过点M作EF∥AC交x轴于E,交y轴于F,
A(-1,0),B(2,0),C(0,-2)
S△ACF=S△ACM=S△ACE=6
∴ CF•OA=6,
CF•OA=6, AE•OC=6
AE•OC=6
∴CF=12,
∴F(0,10),
∴AE=6,
∴E(5,0)
∴直线EF的解析式为:y=-2x+10(6分)
设点M的坐标为(x,x2-x-2)
∵M(x,x2-x-2)在直线EF上
∴x2-x-2=-2x+10
∴x1=3,x2=-4;y1=4,y2=18
∴在抛物线上存在点M使得S△ACM=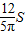 ,且M1(3,4),M2(-4,18).(7分)
,且M1(3,4),M2(-4,18).(7分)
点评:本题考查了抛物线解析式的确定方法,三角形外心的确定及坐标的求法,在抛物线中综合面积问题,求满足条件的点坐标等问题.
 ,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;
,过点(-1,0),可确定二次函数y=ax2-x+c的待定系数a、c,确定解析式;(2)作线段BC和线段AB的垂直平分线,它们的交点就是圆心D,根据点的坐标特点即抛物线的对称轴可求,用勾股定理求半径;
(3)根据(2)可求S=
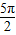 ,故S△ACM=
,故S△ACM=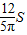 =6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.
=6,用面积法可求满足S△ACM=6的M点所在的直线EF的解析式,再与抛物线联立,得出满足题意的点M.解答:
 解:(1)∵抛物线的对称轴是直线x=
解:(1)∵抛物线的对称轴是直线x=
∴-
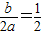
∴a=1,(1分)
∵抛物线向右平移一个单位过坐标原点(0,0),
∴原抛物线过点(-1,0)
∴c=-2
∴抛物线的解析式为y=x2-x-2(2分)
(2)∵OC=OB=2,线段BC的垂直平分线为直线y=-x
∵抛物线的对称轴为直线x=

∴△ABC外接圆⊙D的圆心D(
 ,-
,- )(3分)
)(3分)∵∠ABC=45°,
∴∠ADC=90°
∵AC=
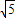 ,
,∴AD=
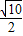 ,
,即△ABC外接圆半径为
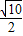 (4分)
(4分)(3)∵S=
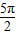 ,
,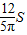 =6,
=6,∴S△ACM=6(5分)
过点M作EF∥AC交x轴于E,交y轴于F,
A(-1,0),B(2,0),C(0,-2)
S△ACF=S△ACM=S△ACE=6
∴
 CF•OA=6,
CF•OA=6, AE•OC=6
AE•OC=6∴CF=12,
∴F(0,10),
∴AE=6,
∴E(5,0)
∴直线EF的解析式为:y=-2x+10(6分)
设点M的坐标为(x,x2-x-2)
∵M(x,x2-x-2)在直线EF上
∴x2-x-2=-2x+10
∴x1=3,x2=-4;y1=4,y2=18
∴在抛物线上存在点M使得S△ACM=
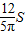 ,且M1(3,4),M2(-4,18).(7分)
,且M1(3,4),M2(-4,18).(7分)点评:本题考查了抛物线解析式的确定方法,三角形外心的确定及坐标的求法,在抛物线中综合面积问题,求满足条件的点坐标等问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的值.
的值.
 .
.