题目内容
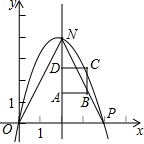 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).(1)求c,b的值,并写出抛物线对称轴及y的最大值(用含有n的代数式表示);
(2)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(3)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
分析:(1)已知抛物线y=-x2+bx+c经过原点O和点P,待定系数法即可求出b和c的值,然后求出抛物线的顶点坐标以及对称轴;
(2)根据抛物线与直线AD交于点N,求出N点的坐标,然后根据三角形的面积公式写出△NPO的面积S关于n的关系式,然后根据面积为1,求出n的值即可;
(3)抛物线经过方形区域ABCD(含边界),则求出抛物线过正方形四个顶点时n的值,然后求出n的取值范围.
(2)根据抛物线与直线AD交于点N,求出N点的坐标,然后根据三角形的面积公式写出△NPO的面积S关于n的关系式,然后根据面积为1,求出n的值即可;
(3)抛物线经过方形区域ABCD(含边界),则求出抛物线过正方形四个顶点时n的值,然后求出n的取值范围.
解答:解:(1)∵抛物线y=-x2+bx+c经过原点O和点P,且p点坐标为(n,0),
∴c=0,b=n,
抛物线的解析式为y=-x2+nx,
抛物线的对称轴x=
,
顶点坐标为(
,
),
y的最大值为
;
(2)∵正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
∴直线AD的解析式为x=2,
∵抛物线与直线AD交于点N,
∴N点的坐标为(2,2n-4),
当n>2时,S△NPO=
×n×(2n-4),
又知△NPO的面积为1,
∴n2-2n=1,
解得n=1±
,
又∵n>0,
∴n=1+
;
当n=2时,P、N两点重合,△NPO不存在,
当0<n<2时,
n(4-2n)=1,解得n=1,
故当n=1+
或n=1时,△NPO的面积为1;
(3)分别把A(2,2)、B(3,2)、C(3,3)、D(2,3)中的横坐标、纵坐标代入抛物线的解析式y=-x2+nx中,
解得n=3;n=
,n=4,n=
,
若抛物线经过正方形区域ABCD(含边界),
则n的取值范围是3≤n≤4.
∴c=0,b=n,
抛物线的解析式为y=-x2+nx,
抛物线的对称轴x=
| n |
| 2 |
顶点坐标为(
| n |
| 2 |
| n2 |
| 4 |
y的最大值为
| n2 |
| 4 |
(2)∵正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).
∴直线AD的解析式为x=2,
∵抛物线与直线AD交于点N,
∴N点的坐标为(2,2n-4),
当n>2时,S△NPO=
| 1 |
| 2 |
又知△NPO的面积为1,
∴n2-2n=1,
解得n=1±
| 2 |
又∵n>0,
∴n=1+
| 2 |
当n=2时,P、N两点重合,△NPO不存在,
当0<n<2时,
| 1 |
| 2 |
故当n=1+
| 2 |
(3)分别把A(2,2)、B(3,2)、C(3,3)、D(2,3)中的横坐标、纵坐标代入抛物线的解析式y=-x2+nx中,
解得n=3;n=
| 11 |
| 3 |
| 7 |
| 2 |
若抛物线经过正方形区域ABCD(含边界),
则n的取值范围是3≤n≤4.
点评:本题主要考查二次函数的综合题的知识点,解答本题(2)问时需要对n进行分类讨论,否则只求出一种答案,解答(3)问时考虑临界的四个顶点,此题有一定的难度.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: