题目内容
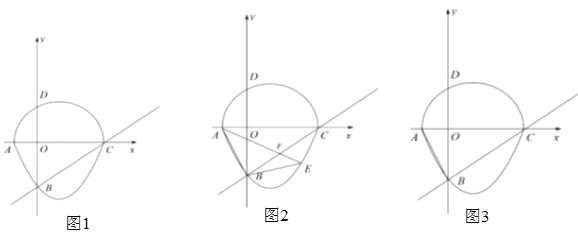
【题目】如图,我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆”,已知![]() 分别为“果圆”与坐标轴的交点,直线
分别为“果圆”与坐标轴的交点,直线![]() 与“果圆”中的抛物线
与“果圆”中的抛物线![]() 交于
交于![]() 两点
两点
(1)求“果圆”中抛物线的解析式,并直接写出“果圆”被![]() 轴截得的线段
轴截得的线段![]() 的长;
的长;
(2)如图,![]() 为直线
为直线![]() 下方“果圆”上一点,连接
下方“果圆”上一点,连接![]() ,设
,设![]() 与
与![]() 交于
交于![]() ,
,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积即为
的面积即为![]() ,求
,求![]() 的最小值
的最小值
(3)“果圆”上是否存在点![]() ,使
,使![]() ,如果存在,直接写出点
,如果存在,直接写出点![]() 坐标,如果不存在,请说明理由
坐标,如果不存在,请说明理由
【答案】(1)![]() ;6;(2)
;6;(2)![]() 有最小值
有最小值![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
(1)先求出点B,C坐标,利用待定系数法求出抛物线解析式,进而求出点A坐标,即可求出半圆的直径,再构造直角三角形求出点D的坐标即可求出BD;
(2)先判断出要求![]() 的最小值,只要CG最大即可,再求出直线EG解析式和抛物线解析式联立成的方程只有一个交点,求出直线EG解析式,即可求出CG,结论得证.
的最小值,只要CG最大即可,再求出直线EG解析式和抛物线解析式联立成的方程只有一个交点,求出直线EG解析式,即可求出CG,结论得证.
(3)求出线段AC,BC进而判断出满足条件的一个点P和点B重合,再利用抛物线的对称性求出另一个点P.
解:(1) 对于直线y=![]() x-3,令x=0,
x-3,令x=0,
∴y=-3,
∴B(0,-3),
令y=0,
∴![]() x-3=0,
x-3=0,
∴x=4,
∴C(4,0),
∵抛物线y=![]() x2+bx+c过B,C两点,
x2+bx+c过B,C两点,
∴
∴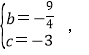
∴抛物线的解析式为y=![]() ;
;
令y=0,
∴![]() =0,
=0,
∴x=4或x=-1,
∴A(-1,0),
∴AC=5,
如图2,记半圆的圆心为O',连接O'D,

∴O'A=O'D=O'C=![]() AC=
AC=![]() ,
,
∴OO'=OC-O'C=4-![]() =
=![]() ,
,
在Rt△O'OD中,OD=![]() =2,
=2,
∴D(0,2),
∴BD=2-(-3)=5;
(2) 如图3,
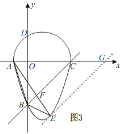
∵A(-1,0),C(4,0),
∴AC=5,
过点E作EG∥BC交x轴于G,
∵△ABF的AF边上的高和△BEF的EF边的高相等,设高为h,
∴S△ABF=![]() AFh,S△BEF=
AFh,S△BEF=![]() EFh,
EFh,
∴![]() =
=![]() =
= ![]()
∵![]() 的最小值,
的最小值,
∴![]() 最小,
最小,
∵CF∥GE,
∴![]()
∴![]() 最小,即:CG最大,
最小,即:CG最大,
∴EG和果圆的抛物线部分只有一个交点时,CG最大,
∵直线BC的解析式为y=![]() x-3,
x-3,
设直线EG的解析式为y=![]() x+m①,
x+m①,
∵抛物线的解析式为y=![]() x2-
x2-![]() x-3②,
x-3②,
联立①②化简得,3x2-12x-12-4m=0,
∴△=144+4×3×(12+4m)=0,
∴m=-6,
∴直线EG的解析式为y=![]() x-6,
x-6,
令y=0,
∴![]() x-6=0,
x-6=0,
∴x=8,
∴CG=4,
∴![]() =
=![]() ;
;
(3)![]() ,
,![]() .理由:
.理由:
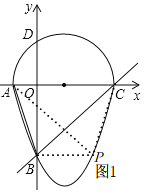
如图1
∴半圆上除点A,C外任意一点Q,都有∠AQC=90°,
∴点P只能在抛物线部分上,
∵B(0,-3),C(4,0),
∴BC=5,
∵AC=5,
∴AC=BC,
∴∠BAC=∠ABC,
当∠APC=∠CAB时,点P和点B重合,即:P(0,-3),
由抛物线的对称性知,另一个点P的坐标为(3,-3),
即:使∠APC=∠CAB,点P坐标为(0,-3)或(3,-3).