题目内容
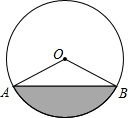 如图是输水管的切面,阴影部分是有水部分,其中水面宽 16cm,最深地方的高度是4cm,求这个圆形切面的半径.
如图是输水管的切面,阴影部分是有水部分,其中水面宽 16cm,最深地方的高度是4cm,求这个圆形切面的半径.分析:设圆形切面的半径为r,过点O作OD⊥AB于点D,交⊙O于点E,由垂径定理可求出BD的长,再根据最深地方的高度是4cm得出OD的长,根据勾股定理即可求出OB的长.
解答: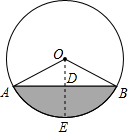 解:设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,
解:设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,
则AD=BD=
AB=
×16=8cm,
∵最深地方的高度是4cm,
∴OD=r=4,
在Rt△OBD中,
OB2=BD2+OD2,即r2=82+(r-4)2,
解得r=10(cm).
答:这个圆形切面的半径是10cm.
 解:设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,
解:设圆形切面的半径,过点O作OD⊥AB于点D,交⊙O于点E,则AD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
∵最深地方的高度是4cm,
∴OD=r=4,
在Rt△OBD中,
OB2=BD2+OD2,即r2=82+(r-4)2,
解得r=10(cm).
答:这个圆形切面的半径是10cm.
点评:本题考查的是垂径定理的应用,解答此类问题的关键是作出辅助线,构造出直角三角形,利用垂径定理及勾股定理进行解答.

练习册系列答案
相关题目
 如图是输水管的切面,阴影部分是有水部分,其中水面宽 16cm,最深地方的高度是4cm,求这个圆形切面的半径.
如图是输水管的切面,阴影部分是有水部分,其中水面宽 16cm,最深地方的高度是4cm,求这个圆形切面的半径.
