Question

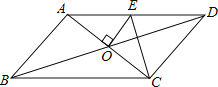
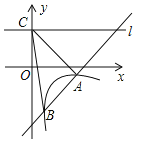
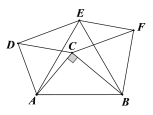
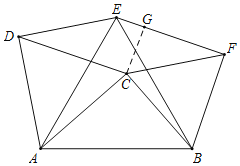
【题目】如图，△ACB中，∠ACB=90°，在AB的同侧分别作正△ACD、正△ABE和正△BCF. 若四边形CDEF的周长是24，面积是17，则AB的长是_______.

Answer 1

【答案】2

【解析】

依据全等三角形的性质，即可得到DE=CB=CF，EF=AC=DC，进而得出四边形CDEF是平行四边形，再根据∠CFG=30°，即可得到CG=CF，进而根据四边形CDEF的周长和面积，得到AC与BC的和与积，再利用勾股定理及完全平方公式的变形即可解答．

如图，过C作CG⊥EF于G，设BC=a，AC=b，
∵△ACD，△ABE，△BCF都是等边三角形，
∴AD=AC，AE=AB，∠DAC=∠EAB=60°，
∴∠DAE=∠CAB，
∴△ADE≌△ACB，
∴DE=CB=CF=a，
同理可得，EF=AC=DC=b，
∴四边形CDEF是平行四边形，
∵∠ACD=∠BCF=60°，∠ACB=90°，
∴∠DCF=150°，
∴∠CFG=30°，

∴CG= CF

∵四边形CDEF的周长是24，面积是17，

∴a+b=12,ab=34

∵∠ACB=90°

∴AB2=

∴AB=2