题目内容
已知正方形ABCD，E、F分别在AD、BC的延长线上，四边形BDEF为菱形，且菱形BDFE的面积为
，则AB=________．
1
分析：设正方形边长为a，菱形BDEF的一条边BD为正方形的对角线，而菱形边长相等，所以菱形的边长为根号a，菱形的高为a，由菱形BDFE的面积为，则可求出a的值．
解答：设正方形边长为a，则
BD=
=a，
∵四边形BDEF为菱形，
∴DE=BD=a，
∵菱形BDFE的面积为，
∴DE•CD=，
∴a•a=，
∴a=1，
∴AB=1，
故答案为1．
点评：本题考查了正方形的性质、菱形的性质以及菱形的面积公式和勾股定理的运用．
分析：设正方形边长为a，菱形BDEF的一条边BD为正方形的对角线，而菱形边长相等，所以菱形的边长为根号
a，菱形的高为a，由菱形BDFE的面积为，则可求出a的值．解答：设正方形边长为a，则
BD=
=a，∵四边形BDEF为菱形，
∴DE=BD=
a，∵菱形BDFE的面积为
，∴DE•CD=
，∴
a•a=，∴a=1，
∴AB=1，
故答案为1．
点评：本题考查了正方形的性质、菱形的性质以及菱形的面积公式和勾股定理的运用．
练习册系列答案
相关题目
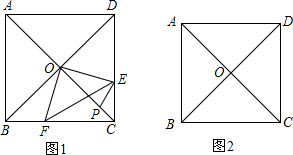
直至点G与点B重合为止．设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2．
已知正方形ABCD的边长为4厘米，E，F分别为边DC，BC上的点，BF=1厘米，CE=2厘米，BE，DF相交于点G，求四边形CEGF的面积．
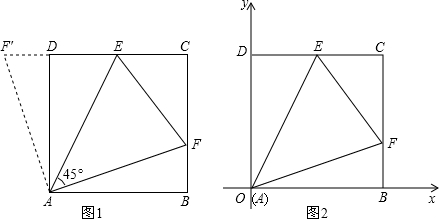
如图，已知正方形ABCD边长为2，E、F、G、H分别为各边上的点，且AE=BF=CG=DH．