Question

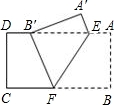
如图，在平行四边形ABCD的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转180°，得到△AB′C．
（1）求证：以A、C、D、B′为顶点的四边形是矩形；
（2）若四边形ABCD的面积S=12cm，求翻转后纸片部分的面积，即S_△ACB．

Answer 1

（1）证明：连接B′D，
∵在?ABCD中，AB=CD，AB∥CD，△ABC沿对角线AC翻转180°，
∴AB′=CD，∠BAC=∠B′AC，
又∵AC⊥CD，
∴∠BAC=∠B′AC=90°，
∴B，A，B′共线，
∴AB′∥CD，
∴四边形ACDB′为平行四边形，
∵∠B′AC=90°
∴?ACDB′为矩形；

（2）∵四边形是ABCD是平行四边形，
∴AB=CD，BC=AD，AC=CA，
∴△ABC≌△CDA，
∴S_△ACB=

1

2

S_?ABCD=

1

2

×12=6．