题目内容
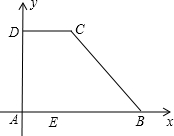 如图,直角梯形ABCD中,点A为坐标原点,B(6,0),BC=5,cosB=
如图,直角梯形ABCD中,点A为坐标原点,B(6,0),BC=5,cosB=| 4 | 5 |
(1)求梯形ABCD的面积和周长;
(2)若点E在线段AB上运动,过点E任作直线,问是否存在直线l将梯形ABCD的周长和面积同时平分?若存在,请求出对应的直线l解析式;若不存在,请说明理由.
分析:(1)如图过C作CF⊥AB于F,这样把梯形分割成矩形和直角三角形,然后解直角三角形BCF,可以求出BF,CF,最后求出梯形ABCD的面积和周长;
(2)存在直线l将梯形ABCD的周长和面积同时平分,设AE=x,可以根据周长和面积平分得到关于x的方程,解方程可以求出x的值,然后结合图形的实际情况判断有三种情况,取舍不存在的情况.
(2)存在直线l将梯形ABCD的周长和面积同时平分,设AE=x,可以根据周长和面积平分得到关于x的方程,解方程可以求出x的值,然后结合图形的实际情况判断有三种情况,取舍不存在的情况.
解答: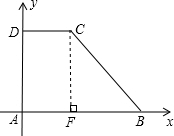 解:(1)过C作CF⊥AB于F,
解:(1)过C作CF⊥AB于F,
∵BC=5,cosB=
,
∴BF=4,CF=3,∴AD=3,
∴AB=6,
∴CD=AF=2,
∴梯形ABCD周长=AB+BC+CD+AD=6+5+2+3=16,
S=
(AB+CD)•AD
=
×8×3=12.
(2)令AE=x,(0≤x≤6),
分三种情况讨论:
①如图,
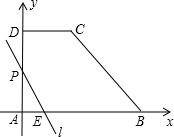
若l与线段AD交于点P,则AP=8-x,
S△AEP=
AE•AP=
x(8-x),
由S△AEP=
S梯形ABCD=6得:
x2-8x+12=0,
解得:x=2或6,即AE=2,AP=6时,直线l将梯形ABCD的周长和面积同时平分,直线l不存在;
当AE=6,AP=2时,直线l将梯形ABCD的周长和面积同时平分.
②如图,
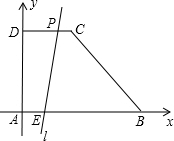
若l与线段DC交于点P,
则DP=5-x,
S四边形AEPD=
(x+5-x)×3=
≠6,
此时直线l不存在.
③如图,

若l与线段BC交于点P,
则BE=6-x,
∵AD+DC+CP+AE=PB+EB,
3+2+5-BP+x=BP+6-x,
∴PB=2+x,
过P作PG⊥AB于G,则
=
,
∴PG=
(2+x),
S△PEB=
(6-x)•
(2+x),
由S△PEB=6得:x2-4x+8=0,
∵△<0,此方程没有实数根,
此时直线l不存在,
综上所述,当AE=6,AP=2时,直线l将梯形ABCD的周长和面积同时平分.
 解:(1)过C作CF⊥AB于F,
解:(1)过C作CF⊥AB于F,∵BC=5,cosB=
| 4 |
| 5 |
∴BF=4,CF=3,∴AD=3,
∴AB=6,
∴CD=AF=2,
∴梯形ABCD周长=AB+BC+CD+AD=6+5+2+3=16,
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
(2)令AE=x,(0≤x≤6),
分三种情况讨论:
①如图,

若l与线段AD交于点P,则AP=8-x,
S△AEP=
| 1 |
| 2 |
| 1 |
| 2 |
由S△AEP=
| 1 |
| 2 |
x2-8x+12=0,
解得:x=2或6,即AE=2,AP=6时,直线l将梯形ABCD的周长和面积同时平分,直线l不存在;
当AE=6,AP=2时,直线l将梯形ABCD的周长和面积同时平分.
②如图,

若l与线段DC交于点P,
则DP=5-x,
S四边形AEPD=
| 1 |
| 2 |
| 15 |
| 2 |
此时直线l不存在.
③如图,

若l与线段BC交于点P,
则BE=6-x,
∵AD+DC+CP+AE=PB+EB,
3+2+5-BP+x=BP+6-x,
∴PB=2+x,
过P作PG⊥AB于G,则
| PG |
| CF |
| PB |
| BC |
∴PG=
| 3 |
| 5 |
S△PEB=
| 1 |
| 2 |
| 3 |
| 5 |
由S△PEB=6得:x2-4x+8=0,
∵△<0,此方程没有实数根,
此时直线l不存在,
综上所述,当AE=6,AP=2时,直线l将梯形ABCD的周长和面积同时平分.
点评:此题比较复杂,尤其是第二问图形的变换与分类讨论,它主要考查了梯形的常用辅助线-作高线,还综合了方程,一次函数,梯形的知识,对学生的要求比较高.

练习册系列答案
相关题目
 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF. ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.