Question

【题目】在中，，，点是边所在直线上的一个动点，与交于点，与边所在直线交于点．

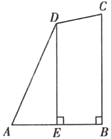
在图①中，，直接写出的值；

在图②中，，直接写出的值；

在图③中，，先写出的值，再加以证明．

Answer 1

【答案】（1）；（2）2；（3）

【解析】

（1）过D作DF⊥BC于F，在△ABC中，∠ABC＝90°，AB＝BC，得到∠ACB＝45°，于是得到DF＝CF，根据AB∥DF，得到比例式，设DF＝CF＝2k，则AC＝BC＝3k，通过△BDF∽△DEF，即可得到结论；
（2）过D作DF⊥BC于F，同理△CDF是等腰直角三角形，通过△ABC≌△DFC，得到AB＝DF，BC＝CF于是得到BF＝2DF，由（1）证得△BDF∽△DEF，列比例式即可得到结论；
（3），如图③过D作DF⊥BC于F，首先证得△DFC是等腰直角三角形，再通过三角形相似得到，设AB＝k，DF＝2k，则BC＝k，CF＝2k，然后由△BDF∽△DEF得到结论．

过作于，

∵在中，，，

∴，

∴是等腰直角三角形，

∴，

∵，

∴，

∴，

∵，

∴，

设，则，

∴，

∵，

∴，

∴；

过作于，

同理是等腰直角三角形，

∴，

∵，

∴，

在与中，，

∴，

∴，，

∴，

∴，

由证得，

∴；

，

如图③，

过作于，

∵在中，，，

∴，

∴是等腰直角三角形，

∴，

∵，

∴，

∴，

∵，

∴，

设，，则，，

∴，

∵，

∴，

∴．