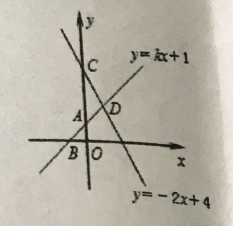ЬтФПФкШн
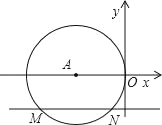
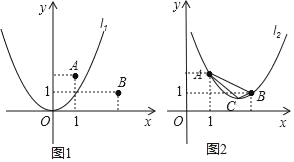
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌЖўДЮКЏЪ§y=x2ЕФЭМЯѓМЧЮЊХзЮяЯпl1ЃЎ
ЃЈ1ЃЉЦНвЦХзЮяЯпl1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЌЕЋВЛОЙ§ЕуBЃЎЧыаДГіЦНвЦКѓХзЮяЯпЕФНтЮіЪНЃЈШЮаДвЛИіМДПЩЃЉЃЛ
ЃЈ2ЃЉЦНвЦХзЮяЯпl1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§AЃЌBСНЕуЃЌМЧЮЊХзЮяЯпl2ЃЌЧѓХзЮяЯпl2ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшХзЮяЯпl2ЕФЖЅЕуЮЊCЃЌKЮЊyжсЩЯвЛЕуЃЎШєSЁїABK=SЁїABCЃЌЧѓЕуKЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x2+1ЃЈ2ЃЉЃЈ0ЃЌ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉПЩНЋХзЮяЯпb1ЯђЩЯЦНвЦЃЌЩшЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+bЃЌгЩЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩЩшХзЮяЯпb2ЕФКЏЪ§ЙиЯЕЪНЮЊy=x2+bx+cЃЌгЩЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЪзЯШИљОнЬтвтЧѓЕУЕуCЕФзјБъЃЌМДПЩЧѓЕУЁїABCЕФУцЛ§ЃЌШЛКѓЗжБ№ДгЕуKдкAЕФЩЯЗНгыЯТЗНШЅЗжЮіЧѓНтЃЌМДПЩЧѓЕУЕуKЕФзјБъЃЎ
НтЃКЃЈ1ЃЉЯђЩЯЦНвЦХзЮяЯпb1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+bЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌ
Ёр2=1+bЃЌ
НтЕУЃКb=1ЃЌ
ЁрЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+1ЃЛ
ЁпЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌ
Ёр32+1Ёй1ЃЌ
ЁрЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+1ЃЛ
ЙЪД№АИЮЊЃКy=x2+1ЃЎ
ЃЈ2ЃЉЩшЁпХзЮяЯпb2ОЙ§AЃЌBСНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК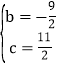 ЃЌ
ЃЌ
ЁрХзЮяЯпb2ЕФКЏЪ§ЙиЯЕЪНЮЊЃКy=x2Љ![]() x+
x+![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпy=x2Љ![]() x+
x+![]() =ЃЈxЉ
=ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуCзїCGЁЭyжсЃЌBFЁЭyжсЃЌAEЁЭyжсЃЌ
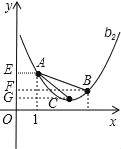
ЁрAE=1ЃЌBF=3ЃЌCG=![]() ЃЌEF=2Љ1=1ЃЌFG=1Љ
ЃЌEF=2Љ1=1ЃЌFG=1Љ![]() =
=![]() ЃЌEG=2Љ
ЃЌEG=2Љ![]() =
=![]() ЃЌ
ЃЌ
ЁрSЁїABC=SЬнаЮABFE+SЬнаЮBCGFЉSЬнаЮACGE=![]() ЃЈAE+BFЃЉEF+
ЃЈAE+BFЃЉEF+![]() ЃЈCG+BFЃЉGFЉ
ЃЈCG+BFЃЉGFЉ![]() ЃЈAE+CGЃЉEG=
ЃЈAE+CGЃЉEG=![]() ЃЌ
ЃЌ
ШєKдкAЕуЩЯЗНЃЌзјБъЮЊЃЈ0ЃЌyЃЉ
SЁїABK=SЁїBNKЉSЁїAMKЉSЬнаЮABNM=![]() BNNKЉ
BNNKЉ![]() AMMKЉ
AMMKЉ![]() ЃЈAM+BNЃЉMN=
ЃЈAM+BNЃЉMN=![]() ЁС3ЁСЃЈyЉ1ЃЉЉ
ЁС3ЁСЃЈyЉ1ЃЉЉ![]() ЁС1ЁСЃЈyЉ2ЃЉЉ
ЁС1ЁСЃЈyЉ2ЃЉЉ![]() ЁСЃЈ1+3ЃЉЁС1=
ЁСЃЈ1+3ЃЉЁС1=![]() ЃЌ
ЃЌ
ЁпSЁїABK=SЁїABCЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃКy=![]() ЃЌ
ЃЌ
дђЕуKЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЭЌРэЃКШєKдкAЕФЯТЗНЪБЃЌдђЕуKЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЁрЕуKЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ