Question

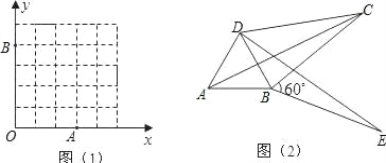
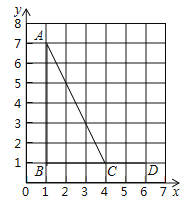
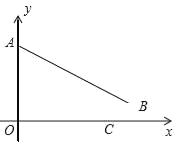
【题目】如图平面直角坐标系中，已知三点 A（0，7），B（8，1），C（x，0）且 0<x <8．

（1）求线段 AB 的长；

（2）请用含 x 的代数式表示 AC+BC 的值；

（3）求 AC+BC 的最小值.

Answer 1

【答案】（1）AB=10；（2）+；（3）AC+BC最小值为8．

【解析】

（1）根据两点间的距离公式可求线段AB的长；

（2）根据两点间的距离公式可求线段AC，BC的值，再相加即可求解；

（3）作B点关于x轴对称点F点，连接AF，与x轴相交于点C．此时AC+BC最短．根据两点间的距离公式即可求解．

（1）；

（2）AC+BC

；

（3）如图，作B点关于x轴对称点F点，连接AF，与x轴相交于点C．此时AC+BC最短．

∵B（8，1），∴F（8，－1），∴AC+BC=AC+CF=AF=．

即AC+BC最小值为8．