题目内容
 如图,在平行四边形OABC中,已知
如图,在平行四边形OABC中,已知 .
.
(1)求点B的坐标;
(2)将平行四边形OABC向左平行移动 个单位长度,再向下平行移动
个单位长度,再向下平行移动 个单位长度,写出所得四边形A′B′C′O′的四个顶点坐标;并求四边形ABCO的面积;
个单位长度,写出所得四边形A′B′C′O′的四个顶点坐标;并求四边形ABCO的面积;
(3)作四边形OABC关于y轴对称图形,并写出对称图形各顶点坐标.
解:(1)∵平行四边形ABCO,
∴AB=OC=2 ,AB∥OC,
,AB∥OC,
∵A( ,
, ),
),
∴B(3 ,
, ),
),
答:B的坐标是(3 ,
, ).
).
(2)A′: -
- =0,
=0, -2
-2 =-
=- ,
,
∴A′(0,- )
)
同理求出B′(2 ,-
,- ),C′(
),C′( ,-2
,-2 ),O′(-
),O′(- ,-2
,-2 ).
).
平行四边形ABCO的面积是2 ×
× =6,
=6,
答:所得四边形A′B′C′O′的四个顶点坐标分别是(0,- ),(2
),(2 ,-
,- ),(
),( ,-2
,-2 ),(-
),(- ,-2
,-2 );四边形ABCO的面积是6.
);四边形ABCO的面积是6.
(3)如图所示:
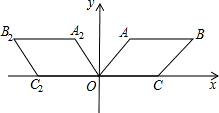
A2、B2、C2、O的坐标分别是:(- ,
, ),(-3
),(-3 ,
, ),(-2
),(-2 ,0),(0,0).
,0),(0,0).
分析:(1)根据平行四边形的性质求出A=OC,AB∥OC,根据A、C的坐标求出即可;
(2)根据平移性质求道即可,根据平行四边形的面积公式和点的坐标即可求出面积.
(3)根据题意画出图形,根据轴对称的性质求出即可.
点评:本题主要考查对平行四边形性质,坐标与图形性质,作图-轴对称变换,坐标与图形变化-平移等知识点的理解和掌握,能熟练地根据性质进行计算是解此题的关键.
∴AB=OC=2
 ,AB∥OC,
,AB∥OC,∵A(
 ,
, ),
),∴B(3
 ,
, ),
),答:B的坐标是(3
 ,
, ).
).(2)A′:
 -
- =0,
=0, -2
-2 =-
=- ,
,∴A′(0,-
 )
)同理求出B′(2
 ,-
,- ),C′(
),C′( ,-2
,-2 ),O′(-
),O′(- ,-2
,-2 ).
).平行四边形ABCO的面积是2
 ×
× =6,
=6,答:所得四边形A′B′C′O′的四个顶点坐标分别是(0,-
 ),(2
),(2 ,-
,- ),(
),( ,-2
,-2 ),(-
),(- ,-2
,-2 );四边形ABCO的面积是6.
);四边形ABCO的面积是6.(3)如图所示:

A2、B2、C2、O的坐标分别是:(-
 ,
, ),(-3
),(-3 ,
, ),(-2
),(-2 ,0),(0,0).
,0),(0,0).分析:(1)根据平行四边形的性质求出A=OC,AB∥OC,根据A、C的坐标求出即可;
(2)根据平移性质求道即可,根据平行四边形的面积公式和点的坐标即可求出面积.
(3)根据题意画出图形,根据轴对称的性质求出即可.
点评:本题主要考查对平行四边形性质,坐标与图形性质,作图-轴对称变换,坐标与图形变化-平移等知识点的理解和掌握,能熟练地根据性质进行计算是解此题的关键.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为