题目内容
【题目】如图，在平面直角坐标系中，直线y=2x与反比例函数y= 
在第一象限内的图象交于点A（m，2），将直线y=2x向下平移后与反比例函数y= 在第一象限内的图象交于点P，且△POA的面积为2． 
（1）求k的值．
（2）求平移后的直线的函数解析式．
【答案】
（1）解：∵点A（m，2）在直线y=2x，
∴2=2m，
∴m=1，
∴点A（1，2），
∵点A（1，2）在反比例函数y= 
上，
∴k=2
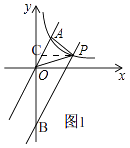
（2）解：方法一、如图，
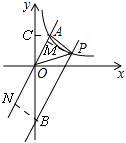
设平移后的直线与y轴相交于B，过点P作PM⊥OA，BN⊥OA，AC⊥y轴
由（1）知，A（1，2），
∴OA= 
，sin∠BON=sin∠AOC= 
= 
，
∵S△POA= 
OA×PM= × PM=2，
∴PM= 
，
∵PM⊥OA，BN⊥OA，
∴PM∥BN，
∵PB∥OA，
∴四边形BPMN是平行四边形，
∴BN=PM= ，
∵sin∠BON= 
= 
= ，
∴OB=4，
∵PB∥AO，
∴B（0，﹣4），
∴平移后的直线PB的函数解析式y=2x﹣4，
方法二、如图1，过点P作PC⊥y轴交OA于C，
设点P的坐标为（n， 
）（n＞1），
∴C（ 
， ），∴PC=n﹣ ，
∵△POA的面积为2．A（1，2）
∴S△POA=S△PCO+S△PCA
= （n﹣ ）× + （n﹣ ）（2﹣ ）
= （n﹣ ）×2
=n﹣
=2，
∴n=1﹣ 
（舍）或n=1+ ，
∴P（1+ ，2 ﹣2）
∴PB∥AO，
∴设直线PB的解析式为y=2x+b，
∵点P在直线PB上，
∴2 ﹣2=2（1+ ）+b，
∴b=﹣4，
∴平移后的直线PB的函数解析式y=2x﹣4，
【解析】（1）由点A的纵坐标求得m，即点A的坐标，把点A的坐标代入反比例函数中即可；（2）方法一、先求出PM，再求出BN然后用锐角三角函数求出OB，即可．方法二、先设出点P的坐标，利用△POA的面积为2．建立方程求出点P的坐标，即可得出结论．
【题目】甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
根据以上信息，整理分析数据如下：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
（1）写出表格中a，b，c的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
