题目内容
给出下列命题:
①若m=n+1,则1-m2+2mn-n2=0;②对于函数y=kx+b(k≠0),若y随x的增大而增大,则其图象不能同时经过第二、四象限;③若a、b(a≠b)为2、3、4、5这四个数中的任意两个,则满足2a-b>4的有序数组(a,b)共有5组.
其中所有正确命题的序号是 .
①若m=n+1,则1-m2+2mn-n2=0;②对于函数y=kx+b(k≠0),若y随x的增大而增大,则其图象不能同时经过第二、四象限;③若a、b(a≠b)为2、3、4、5这四个数中的任意两个,则满足2a-b>4的有序数组(a,b)共有5组.
其中所有正确命题的序号是
考点:命题与定理
专题:
分析:利用完全平方公式、一次函数的性质及不等式的解分别判断后即可确定正确的选项.
解答:解:∵m=n+1,
∴m-n=1,
∴1-m2+2mn-n2=0,
故正确;
②对于函数y=kx+b(k≠0),若y随x的增大而增大,则其图象不能同时经过第二、四象限,错误;
③若a、b(a≠b)为2、3、4、5这四个数中的任意两个,则满足2a-b>4的有序数组(a,b)共有5组,正确.
故答案为:①③
∴m-n=1,
∴1-m2+2mn-n2=0,
故正确;
②对于函数y=kx+b(k≠0),若y随x的增大而增大,则其图象不能同时经过第二、四象限,错误;
③若a、b(a≠b)为2、3、4、5这四个数中的任意两个,则满足2a-b>4的有序数组(a,b)共有5组,正确.
故答案为:①③
点评:本题考查了命题与定理的知识,解题的关键是了解完全平方公式、一次函数的性质及不等式的解等知识,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两圆半径分别是方程x2-7x+10=0的两根,两圆的圆心距为6,则两圆的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
-2015的相反数是( )
A、
| ||
| B、2015 | ||
| C、-2015 | ||
D、-
|
方程3(x-1)=
的解是( )
| 1 |
| 2 |
A、x=
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个.如果每人做4个,那么比计划少15个,若用方程描述其中数量之间的相等关系,设他们计划做x个“中国结”,则得方程( )
| A、5x-9=4x+15 | ||||
| B、5x+9=4x-15 | ||||
C、
| ||||
D、
|
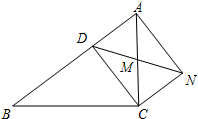 如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC. 如图,已知∠ACB=∠F,BE=CF,添加一个合适的条件,如
如图,已知∠ACB=∠F,BE=CF,添加一个合适的条件,如