题目内容
已知多项式-m3n2-2中,含字母的项的系数为a,多项式的次数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.
(1)求a、b、c的值,并在数轴上标出A、B、C;
(2)若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动,它们的速度分别是
个单位长度/秒、2个单位长度/秒、
个单位长度/秒,当乙追上丙时,乙是否追上了甲?为什么?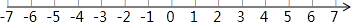
(1)求a、b、c的值,并在数轴上标出A、B、C;
(2)若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动,它们的速度分别是
| 1 |
| 2 |
| 1 |
| 4 |
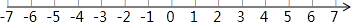
分析:(1)根据多项式的相关概念,求出含字母的项的系数、多项式的次数和常数项,即可得出a,b,c的值,并在数轴上表示出来;
(2)根据数轴上两点间的距离的求法列方程进行求解即可;
(2)根据数轴上两点间的距离的求法列方程进行求解即可;
解答:解:(1)∵多项式-m3n2-2中,含字母的项的系数为-1,次数为5,常数项为-2,
∴a=-1,b=5,c=-2,
在数轴上表示如下:

(2)当乙追上丙时,乙也刚好追上了甲.
由题意知道:AB=6,AC=1,BC=7.
设乙用x秒追上丙,
则2x-
x=7,
解得:x=4.
∴当乙追上丙时,甲运动了
×4=2个单位长度,乙运动了2×4=8个单位长度,
此时恰好有AB+2=8,
∴乙同时追上甲和丙.
∴a=-1,b=5,c=-2,
在数轴上表示如下:

(2)当乙追上丙时,乙也刚好追上了甲.
由题意知道:AB=6,AC=1,BC=7.
设乙用x秒追上丙,
则2x-
| 1 |
| 4 |
解得:x=4.
∴当乙追上丙时,甲运动了
| 1 |
| 2 |
此时恰好有AB+2=8,
∴乙同时追上甲和丙.
点评:此题考查了一元一次方程的应用,用到的知识点是多项式的有关概念、数轴、一元一次方程,关键是根据题目中的数量关系,列出方程.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ,2,
,2, (单位长度/秒),当乙追上丙时,乙是否追上了甲?为什么?
(单位长度/秒),当乙追上丙时,乙是否追上了甲?为什么?