题目内容
 如图,已知:AD平分∠BAC,AC=AB+BD,∠B=56°,则∠C=
如图,已知:AD平分∠BAC,AC=AB+BD,∠B=56°,则∠C=分析:在AC上取一点E,使AE=AB,连接DE,由条件就可以得出△ADB≌△ADE,就可以得出BD=DE,就可以得出DE=CE,由三角形的外角与内角的关系就可以得出∠C的值.
解答:解: 在AC上取一点E,使AE=AB,连接DE,
在AC上取一点E,使AE=AB,连接DE,
∵AD平分∠BAC,
在△ADB和△ADE中
.
∴△ADB≌△ADE(SAS),
∴BD=ED.∠B=∠AED=56°.
∵AC=AB+BD,AC=AE+EC
∴AB+BD=AE+CE,
∴BD=CE,
∴DE=CE.
∴∠CDE=∠C.
∵∠C+∠CDE=∠AED,
∴2∠C=56°,
∴∠C=28°.
故答案为:28°.
 在AC上取一点E,使AE=AB,连接DE,
在AC上取一点E,使AE=AB,连接DE,∵AD平分∠BAC,
在△ADB和△ADE中
|
∴△ADB≌△ADE(SAS),
∴BD=ED.∠B=∠AED=56°.
∵AC=AB+BD,AC=AE+EC
∴AB+BD=AE+CE,
∴BD=CE,
∴DE=CE.
∴∠CDE=∠C.
∵∠C+∠CDE=∠AED,
∴2∠C=56°,
∴∠C=28°.
故答案为:28°.
点评:本题考查了角平方形的性质的运用,全等三角形的判定及性质的运用,三角形的外角与内角的关系的运用.解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由.
如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由.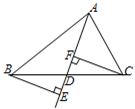 27、如图,已知BE⊥AD,CF⊥AD,且BE=CF.
27、如图,已知BE⊥AD,CF⊥AD,且BE=CF.
 如图,已知:AD平分∠BAC,AC=AB+BD,∠B=56°,则∠C=________.
如图,已知:AD平分∠BAC,AC=AB+BD,∠B=56°,则∠C=________.