题目内容
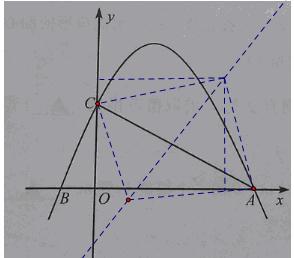
在平面直角坐标系 中,二次函数
中,二次函数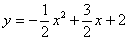 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C.过动点H(0,
轴交于点C.过动点H(0,  )作平行于
)作平行于 轴的直线,直线与二次函数
轴的直线,直线与二次函数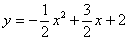 的图像相交于点D,E.
的图像相交于点D,E.
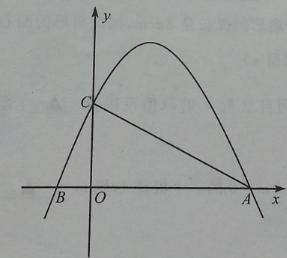
(1)写出点A,点B的坐标;
(2)若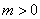 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与 轴相切时,求
轴相切时,求 的值;
的值;
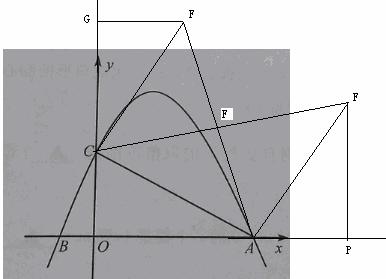
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(1)当 =0时,有
=0时,有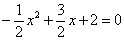 ,解之得:
,解之得: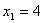 ,
,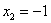 ,∴A、B两点的坐标分别为(4,0)和(-1,0).
,∴A、B两点的坐标分别为(4,0)和(-1,0).
(2)∵⊙Q与 轴相切,且与
轴相切,且与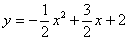 交于D、E两点,
交于D、E两点,
∴圆心O位于直线与抛物线对称轴的交点处,且⊙Q的半径为H点的纵坐标 (
(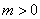 )
)
∵抛物线的对称轴为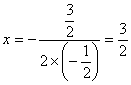 ,
,
∴D、E两点的坐标分别为:(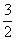 -
- ,
, ),(
),(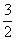 +
+ ,
, )且均在二次函数
)且均在二次函数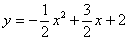 的图像上,
的图像上,
∵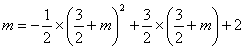 ,解得
,解得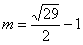 或
或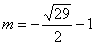 (不合题意,舍去)
(不合题意,舍去)
(3)存在.
①当∠ACF=90°,AC=FC时,过点F作FG⊥ 轴于G,∴∠AOC=∠CGF=90°,
轴于G,∴∠AOC=∠CGF=90°,
∵∠ACO+∠FCG=90°,∠GFC+∠FCG=90°,∴∠ACO=∠CFG,∴△ACO≌△∠CFG,∴CG=AO=4,
∵CO=2,∴ =OG=2+4=6;
=OG=2+4=6;
②当∠CAF=90°,AC=AF时,过点F作FP⊥ 轴于P,∴∠AOC=∠APF=90°,
轴于P,∴∠AOC=∠APF=90°,
∵∠ACO+∠OAC=90°,∠FAP+∠OAC=90°,∴∠ACO=∠FAP,∴△ACO≌△∠FAP,∴FP =AO=4,
∴ =FP =4;
=FP =4;
③当∠AFC=90°,FA=FC时,则F点一定在AC的中垂线上,此时 =3或
=3或 =1
=1

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,直线l∥OB,则∠1的度数是( )

|
| A. | 120° | B. | 30 | C. | 40° | D. | 60° |
 .
.
 的图像经过点P(1,1),与
的图像经过点P(1,1),与 ∠ABO=3,那么A点的坐标是 .
∠ABO=3,那么A点的坐标是 .
 与最接近的是········································································ ( )
与最接近的是········································································ ( ) 的结果是____.
的结果是____. °
° |+
|+ ﹣(
﹣(