题目内容
如图，直线AB与CD相交于点O，OE⊥AB，若∠BOD：∠DOE=1：4，求∠COE．
解：∵∠BOD：∠DOE=1：4，∠BOD+∠DOE=90°，
∴∠BOD=90°×
=18°，∠DOE=90°×
=72°．
∴∠COE=180°-∠DOE=108°．
分析：根据∠BOD：∠DOE=1：4和∠BOD+∠DOE=90°，即可求得∠BOD和∠DOE，再进一步根据平角定义求得∠COE．
点评：此题考查了余角和补角的计算方法，注意领会由垂直得直角这一要点．
∴∠BOD=90°×
=18°，∠DOE=90°×=72°．∴∠COE=180°-∠DOE=108°．
分析：根据∠BOD：∠DOE=1：4和∠BOD+∠DOE=90°，即可求得∠BOD和∠DOE，再进一步根据平角定义求得∠COE．
点评：此题考查了余角和补角的计算方法，注意领会由垂直得直角这一要点．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
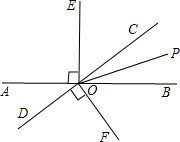如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD．
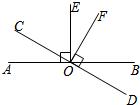8、如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD．则图中除了直角相等外，还有相等的角，请写出三对：
10、如图，直线AB与CD相交于O点，且∠COE=90°，则与∠EOA互余的角有
如图，直线AB与CD相交于点O，∠AOC=65°，则∠DOB=