Question

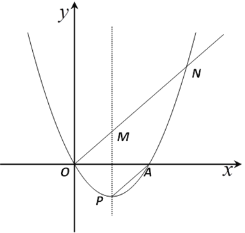
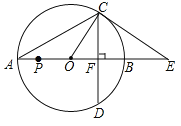
【题目】已知在平面直角坐标系中，点，以线段为直径作圆，圆心为，直线交于点，连接.

（1）求证：直线是的切线；

（2）点为轴上任意一动点，连接交于点，连接：

①当时，求所有点的坐标 （直接写出）；

②求的最大值.

Answer 1

【答案】（1）见解析；（2）①，；② 的最大值为.

【解析】

（1）连接，证明∠EDO=90°即可；

（2）①分“位于上”和“位于的延长线上”结合相似三角形进行求解即可；

②作于点，证明，得，从而得解.

（1）证明：连接，则：

∵为直径

∴

∴

∵

∴

∴

∵

∴

∴

即：

∵轴

∴

∴

∴直线为的切线.

（2）①如图1，当位于上时：

∵

∴

∴设，则

∴

∴，解得：

∴

即

如图2，当位于的延长线上时：

∵

∴设，则

∴

∴

解得：

∴

即

②如图，作于点，

∵是直径

∴

∴

∴

∵半径

∴

∴的最大值为.