ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯп
жаЃЌХзЮяЯп![]() ЃЎ
ЃЎ
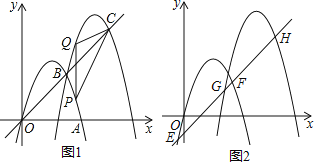
ЃЈ1ЃЉШєИУХзЮяЯпгыжБЯп![]() НЛгкAЃЌBСНЕуЃЌЕуBдкyжсЩЯЃЎЧѓИУХзЮяЯпЕФБэДяЪНМАЕуAЕФзјБъЃЛ
НЛгкAЃЌBСНЕуЃЌЕуBдкyжсЩЯЃЎЧѓИУХзЮяЯпЕФБэДяЪНМАЕуAЕФзјБъЃЛ
ЃЈ2ЃЉКсзјБъЮЊећЪ§ЕФЕуГЦЮЊКсећЕуЃЎ
ЂйНЋЃЈ1ЃЉжаЕФХзЮяЯпдкAЃЌBСНЕужЎМфЕФВПЗжМЧзї![]() ЃЈВЛКЌAЃЌBСНЕуЃЉЃЌжБНгаДГі
ЃЈВЛКЌAЃЌBСНЕуЃЉЃЌжБНгаДГі![]() ЩЯЕФКсећЕуЕФзјБъЃЛ
ЩЯЕФКсећЕуЕФзјБъЃЛ
ЂкХзЮяЯп![]() гыжБЯп
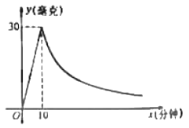
гыжБЯп![]() НЛгкCЃЌDСНЕуЃЌНЋХзЮяЯпдкCЃЌDСНЕужЎМфЕФВПЗжМЧзї
НЛгкCЃЌDСНЕуЃЌНЋХзЮяЯпдкCЃЌDСНЕужЎМфЕФВПЗжМЧзї![]() ЃЈВЛКЌCЃЌDСНЕуЃЉЃЌШє
ЃЈВЛКЌCЃЌDСНЕуЃЉЃЌШє![]() ЩЯЧЁгаСНИіКсећЕуЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЩЯЧЁгаСНИіКсећЕуЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
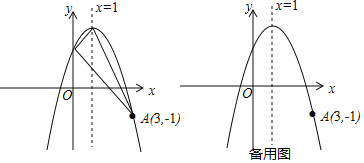
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌAзјБъЮЊЃЈ-4ЃЌ2ЃЉЃЛЃЈ2ЃЉЂйЃЈ-3ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ-2ЃЉЃЌЃЈ-1ЃЌ-1ЃЉЃЛ
ЃЌAзјБъЮЊЃЈ-4ЃЌ2ЃЉЃЛЃЈ2ЃЉЂйЃЈ-3ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ-2ЃЉЃЌЃЈ-1ЃЌ-1ЃЉЃЛ
Ђк![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌЕУBзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌАбBЕФзјБъДњШы![]() ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйАбx=-3ЃЌx=-2ЃЌx=-1ЃЌДњШы![]() ЃЌМДПЩЃЛ
ЃЌМДПЩЃЛ
ЂкСЊСЂ![]() гы
гы![]() ЃЌЕУЃК
ЃЌЕУЃК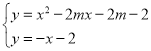 ЃЌЕУCЃЌDЕузјБъЗжБ№ЪЧЃКЃЈ-1ЃЌ-1ЃЉЃЌЃЈ2mЃЌ-2m-2ЃЉЃЌНјЖјПЩЧѓЕУmЕФЗЖЮЇ.
ЃЌЕУCЃЌDЕузјБъЗжБ№ЪЧЃКЃЈ-1ЃЌ-1ЃЉЃЌЃЈ2mЃЌ-2m-2ЃЉЃЌНјЖјПЩЧѓЕУmЕФЗЖЮЇ.
ЃЈ1ЃЉЁпХзЮяЯпгыжБЯп![]() НЛгкAЃЌBСНЕуЃЌЕуBдкyжсЩЯЃЌ
НЛгкAЃЌBСНЕуЃЌЕуBдкyжсЩЯЃЌ
ЁрBзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌ
АбBЃЈ0ЃЌ2ЃЉДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЃЌНтЕУЃКm=-2ЃЌ
ЃЌНтЕУЃКm=-2ЃЌ
ЁрХзЮяЯпЕУНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЕБy=2ЪБЃЌ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрAзјБъЮЊЃЈ-4ЃЌ2ЃЉЃЌ
ЃЈ2ЃЉЂйЁпAзјБъЮЊЃЈ-4ЃЌ2ЃЉЃЌBзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌ
ЁрЕБx=-3ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБx=-2ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБx=-1ЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЩЯЕФКсећЕуЕФзјБъЪЧЃКЃЈ-3ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ-2ЃЉЃЌЃЈ-1ЃЌ-1ЃЉ
ЩЯЕФКсећЕуЕФзјБъЪЧЃКЃЈ-3ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ-2ЃЉЃЌЃЈ-1ЃЌ-1ЃЉ
ЂкСЊСЂ![]() гы
гы![]() ЃЌЕУЃК
ЃЌЕУЃК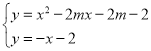 ЃЌ
ЃЌ
Ёр![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрCЃЌDЕузјБъЗжБ№ЪЧЃКЃЈ-1ЃЌ-1ЃЉЃЌЃЈ2mЃЌ-2m-2ЃЉЃЌ
Ёп![]() ЩЯЧЁгаСНИіКсећЕуЃЌ
ЩЯЧЁгаСНИіКсећЕуЃЌ
ЁрСНИіКсећЕуЕФКсзјБъЮЊЃКx=0ЃЌx=1Лђx=-2ЃЌx=-3ЃЌ
Ёр![]() Лђ
Лђ![]()
Ёр![]() Лђ
Лђ![]() .
.