Question

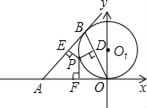
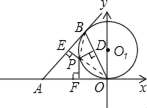
【题目】如图，OB是以（O，a）为圆心，a为半径的⊙O1的弦，过B点作⊙O1的切线，P为劣弧上的任一点，且过P作OB、AB、OA的垂线，垂足分别是D、E、F．

（1）求证：PD2=PEPF；

（2）当∠BOP=30°，P点为OB的中点时，求D、E、F、P四个点的坐标及S△DEF．

Answer 1

【答案】（1）详见解析；（2）D（﹣a， a），E（﹣a， a），F（﹣a，0），P（﹣a， ）；S△DEF=a2．

【解析】试题分析：（1）连接PB，OP，利用AB切⊙O1于B求证△PBE∽△POD，得出，同理，△OPF∽△BPD，得出，然后利用等量代换即可．
（2）连接O1B，O1P，得出△O1BP和△O1PO为等边三角形，根据直角三角形的性质即可解得D、E、F、P四个点的坐标．再利用三角形的面积公式可直接求出三角形DEF的面积．

试题解析：（1）证明：连接PB，OP，

∵PE⊥AB，PD⊥OB，

∴∠BEP=∠PDO=90°，

∵AB切⊙O1于B，∠ABP=∠BOP，

∴△PBE∽△POD，

∴=，

同理，△OPF∽△BPD

∴=，

∴=，

∴PD2=PEPF；

（2）连接O1B，O1P，

∵AB切⊙O1于B，∠POB=30°，

∴∠ABP=30°，

∴∠O1BP=90°﹣30°=60°，

∵O1B=O1P，

∴△O1BP为等边三角形，

∴O1B=BP，

∵P为弧BO的中点，

∴BP=OP，

即△O1PO为等边三角形，

∴O1P=OP=a，

∴∠1OP=60°，

又∵P为弧BO的中点，

∴O1P⊥OB，

在△O1DO中，∵∠O1OP=60°O1O=a，

∴O1D=a，OD=a，

过D作DM⊥OO1于M，∴DM=OD=a，

OM=DM=a，

∴D（﹣a， a），

∵∠O1OF=90°，∠O1OP=60°

∴∠POF=30°，

∵PE⊥OA，

∴PF=OP=a，OF=a，

∴P（﹣a，），F（﹣a，0），

∵AB切⊙O1于B，∠POB=30°，

∴∠ABP=∠BOP=30°，

∵PE⊥AB，PB=a，

∴∠EPB=60°

∴PE=a，BE=a，

∵P为弧BO的中点，

∴BP=PO，

∴∠PBO=∠BOP=30°，

∴∠BPO=120°，

∴∠BPE+∠BPO=120°+60°=180°，

即OPE三点共线，

∵OE=a+a=a，

过E作EM⊥x轴于M，∵AO切⊙O1于O，

∴∠EOA=30°，

∴EM=OE=a，OM=a，

∴E（﹣a， a），

∵E（﹣a， a），D（﹣a， a），

∴DE=﹣a﹣（﹣a）=a，

DE边上的高为： a，

∴S△DEF=×a×a=a2．

故答案为：D（﹣a， a），E（﹣a， a），F（﹣a，0），P（﹣a，）；S△DEF=a2．