题目内容
已知反比例函数y=| m-2 |
| x |
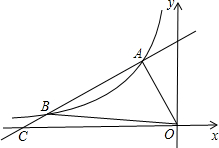 C与函数y=
C与函数y=| m-2 |
| x |
(1)求m的值及点B的坐标:
(2)求△AOB的面积.
分析:(1)把点A的坐标代入反比例函数解析式可得m的值,过A、B向x轴引垂线,构造三角形相似,易得点B的纵坐标,进而代入反比例函数解析式可得B的横坐标;
(2)由A、B两点的坐标可得直线AB的解析式,可得点C的坐标,S△AOB=S△AOC-S△BOC.
(2)由A、B两点的坐标可得直线AB的解析式,可得点C的坐标,S△AOB=S△AOC-S△BOC.
解答:解:把点A(-2,3)代入y=
,
得m=-4.
作BD⊥OC于D,AE⊥OC于E.
∴△BDC∽△AEC,
∴
=
,
∵AB=2BC,
∴
=
,
∵AE=3,
∴BD=1,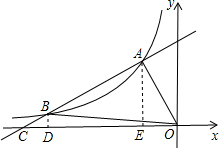
当y=1时,x=-6,
∴B(-6,1);
(2)由A(-2,3)、B(-6,1)得直线AB的解析式为y=
x+4,
∴C(-8,0),
∴S△AOB=S△AOC-S△BOC=
×8×3-
×8×1=8.
| m-2 |
| x |
得m=-4.
作BD⊥OC于D,AE⊥OC于E.
∴△BDC∽△AEC,
∴
| BD |
| AE |
| BC |
| AC |
∵AB=2BC,
∴
| BD |
| AE |
| 1 |
| 3 |
∵AE=3,
∴BD=1,

当y=1时,x=-6,
∴B(-6,1);
(2)由A(-2,3)、B(-6,1)得直线AB的解析式为y=
| 1 |
| 2 |
∴C(-8,0),
∴S△AOB=S△AOC-S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题综合考查了反比例函数与一次函数相交问题;利用相似三角形的知识得到B的坐标为解决本题的突破点.

练习册系列答案
相关题目
 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 已知反比例函数
已知反比例函数