题目内容
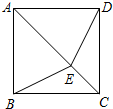 如图,E为正方形ABCD对角线AC上一点,若AE=BC,则∠BED等于
如图,E为正方形ABCD对角线AC上一点,若AE=BC,则∠BED等于
- A.115°
- B.125°
- C.135°
- D.150°
C
分析:根据正方形的性质可知:AB=BC,因为AE=BC,所以AB=AE,即三角形ABE是等腰三角形,因为∠BAE是45°,所以可求出∠BEA,同理可求出∠AED的度数,进而求出∠BED的度数.
解答:∵四边形ABCD是正方形,AC是对角线,
∴AB=BC,∠BAE=45°,
∵AE=BC,
∴∠ABE=∠AED= =67.5°,
=67.5°,
同理可求得:∠AED=67.5°,
∴∠BED=2×67.5°=135°.
故选C.
点评:本题考查了正方形的性质:四边相等、对角线平分对角以及等腰三角形的判定和性质和三角形内角和定理的运用.
分析:根据正方形的性质可知:AB=BC,因为AE=BC,所以AB=AE,即三角形ABE是等腰三角形,因为∠BAE是45°,所以可求出∠BEA,同理可求出∠AED的度数,进而求出∠BED的度数.
解答:∵四边形ABCD是正方形,AC是对角线,
∴AB=BC,∠BAE=45°,
∵AE=BC,
∴∠ABE=∠AED=
 =67.5°,
=67.5°,同理可求得:∠AED=67.5°,
∴∠BED=2×67.5°=135°.
故选C.
点评:本题考查了正方形的性质:四边相等、对角线平分对角以及等腰三角形的判定和性质和三角形内角和定理的运用.

练习册系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以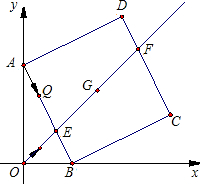 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.