题目内容
已知四边形ABCD,以此四边形的四条边为边向外分别作正方形,顺次连结这四个正方形的对角线交点E,F,G,H,得到一个新四边形EFGH.
(1)如图1,若四边形ABCD是正方形,则四边形EFGH( )(填“是”或“不是”)正方形;
(2)如图2,若四边形ABCD是矩形,则(1)中的结论( )(填“能”或“不能”)成立;
(3)如图3,若四边形ABCD是平行四边形,其他条件不变, 判断(1)中的结论是否还成立?若成立,证明你的结论,若不成立,请说明你的理由.
(2)如图2,若四边形ABCD是矩形,则(1)中的结论( )(填“能”或“不能”)成立;
(3)如图3,若四边形ABCD是平行四边形,其他条件不变, 判断(1)中的结论是否还成立?若成立,证明你的结论,若不成立,请说明你的理由.

(1)是 ; (2)能 ;
(3)证明:连结EF,FG,GH,HE,AE,AH,DG,DH,
∵四边形ABCD是平行四边形,
∴AB=CD,即以AB,CD分别为边的正方形的对角线也相等.
∵点E,G是上述两个正方形的对角线交点,
∴AE=DG.
∵点H是以AD为一边的正方形的对角线交点,
∴AH=DH. 易知
∵平行四边形ABCD中,有
∴
∴
∴
∴HG=HE且
同理可证HE=EF=FG. ∴四边形EFGH是菱形.
∵点H是正方形的对角线交点, ∴, 即.
即. 
∴.
∴四边形EFGH是正方形.
(3)证明:连结EF,FG,GH,HE,AE,AH,DG,DH,
∵四边形ABCD是平行四边形,
∴AB=CD,即以AB,CD分别为边的正方形的对角线也相等.
∵点E,G是上述两个正方形的对角线交点,
∴AE=DG.
∵点H是以AD为一边的正方形的对角线交点,
∴AH=DH. 易知

∵平行四边形ABCD中,有

∴

∴

∴

∴HG=HE且

同理可证HE=EF=FG. ∴四边形EFGH是菱形.
∵点H是正方形的对角线交点, ∴,
 即.
即. 
∴.

∴四边形EFGH是正方形.

练习册系列答案
相关题目
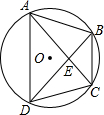 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |
如图,已知四边形ABCD是边长为2的正方形,E是AB的中点,F是BC的中点,AF与DE相交于G,BD和AF相交于H,那么四边形BEGH的面积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
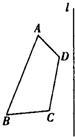 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.