Question

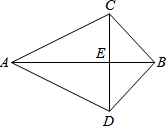如图，已知AC=AD，BC=BD，则全等三角形共有（　　）对．

A．1

B．2

C．3

D．4

Answer 1

分析：首先证明△ABC≌△ADC，根据全等三角形的性质可得∴∠CAE=∠DAE，∠CBA=∠DBA，再证明△AEC≌△AED，△CBE≌△DBE．

解答：解：∵在△ABC和△ABD中

AC=AD AB=AB BC=BD

，
∴△ABC≌△ABD（SSS），
∴∠CAE=∠DAE，∠CBA=∠DBA，
∵在△AEC和△AED中

AC=AD ∠CAE=∠DAE AE=AE

，
∴△AEC≌△AED（SAS），
在△CBE和△DBE中

BC=BD ∠CBE=∠DBE EB=EB

，
∴△CBE≌△DBE（SAS），
故选：C．

点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．