题目内容
某班共有48人，人人都会下棋，会下象棋的人数是会下围棋人数的2倍少3人，两种棋都会下的至多9人，但不少于5人，则会下围棋的有
- A.20人
- B.19人
- C.11人或13人
- D.19人或20人
D
分析：设会下围棋的有x人，则会下象棋的有（2x-3）人，由两种棋都会下的至多9人，但不少于5人，可得出不等式组，解出即可．
解答：设会下围棋的有x人，则会下象棋的有（2x-3）人，
由题意得：5≤x+（2x-3）-48≤9，
解得：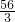
≤x≤20，
故可得会下围棋的人数有19人或20人．
故选D．
点评：本题考查了一元一次不等式组的应用，解答本题的关键是表示出两种棋都会下的人数，有一定难度．
分析：设会下围棋的有x人，则会下象棋的有（2x-3）人，由两种棋都会下的至多9人，但不少于5人，可得出不等式组，解出即可．
解答：设会下围棋的有x人，则会下象棋的有（2x-3）人，
由题意得：5≤x+（2x-3）-48≤9，
解得：
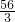≤x≤20，故可得会下围棋的人数有19人或20人．
故选D．
点评：本题考查了一元一次不等式组的应用，解答本题的关键是表示出两种棋都会下的人数，有一定难度．
练习册系列答案
相关题目