Question

已知抛物线y=ax²+bx+c（0＜2a＜b）的顶点为P（x₀，y₀），点A（1，y_A）、B（0，y_B）、C（－1，y_C）在该抛物线上．
（Ⅰ）当a=1，b=4，c=10时，①求顶点P的坐标；②求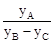-的值；
（Ⅱ）当y₀≥0恒成立时，求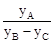的最小值．

Answer 1

（Ⅰ）若a=1，b=4，c=10，此时抛物线的解析式为y=x²+4x+10。
①∵y=x²+4x+10=（x+2）²+6，∴抛物线的顶点坐标为P（－2，6）。
②∵点A（1，y_A）、B（0，y_B）、C（－1，y_C）在抛物线y=x²+4x+10上，
∴y_A=15，y_B=10，y_C=7。∴。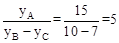
（Ⅱ）由0＜2a＜b，得。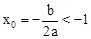
由题意，如图过点A作AA₁⊥x轴于点A₁，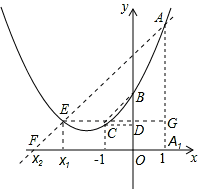

则AA₁=y_A，OA₁=1。
连接BC，过点C作CD⊥y轴于点D，
则BD=y_B－y_C，CD=1。
过点A作AF∥BC，交抛物线于点E（x₁，y_E），交x轴于点F（x₂，0）。
则∠FAA₁=∠CBD。∴Rt△AFA₁∽Rt△BCD。
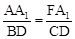∴，即。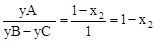
过点E作EG⊥AA₁于点G，易得△AEG∽△BCD。
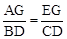∴，即。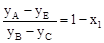
∵点A（1，y_A）、B（0，y_B）、C（－1，y_C）、E（x₁，y_E）在抛物线y=ax²+bx+c上，
∴y_A=a+b+c，y_B=c，y_C=a－b+c，y_E=ax₁²+bx₁+c，
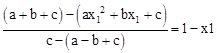∴，化简，得x₁²＋x₁－2=0，
解得x₁=－2（x₁=1舍去）。
∵y₀≥0恒成立，根据题意，有x₂≤x₁＜－1。
则1－x₂≥1－x₁，即1－x₂≥3。
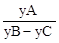∴的最小值为3。

解析