题目内容
如图所示，一个直角三角尺的斜边AB=25cm，一条直角边AC=20cm，以AB为轴，将这个三角尺旋转一周，形成如图所示的一个旋转体，这个旋转体的全面积是
- A.320πcm2
- B.420πcm2
- C.280πcm2
- D.160πcm2
B
分析：易得这个几何体为两个圆锥的组合，需求得底面半径．如图，作CD⊥AB，由勾股定理求得CB的长，由射影定理求得BD后，再由等积法求得CD，根据扇形的面积公式求得圆锥的全面积．
解答：
解：∵AB=25cm，AC=20cm，
∴CB=
=15cm，
作CD⊥AB，垂足为D．
∴CD=
=
=12，
∴S=π•CD•AC+π•CD•BC=π•CD•（AC+BC）=420πcm2．
故选B．
点评：本题利用了勾股定理，射影定理，扇形的面积公式求解．
分析：易得这个几何体为两个圆锥的组合，需求得底面半径．如图，作CD⊥AB，由勾股定理求得CB的长，由射影定理求得BD后，再由等积法求得CD，根据扇形的面积公式求得圆锥的全面积．
解答：
解：∵AB=25cm，AC=20cm，∴CB=
=15cm，作CD⊥AB，垂足为D．
∴CD=
==12，∴S=π•CD•AC+π•CD•BC=π•CD•（AC+BC）=420πcm2．
故选B．
点评：本题利用了勾股定理，射影定理，扇形的面积公式求解．
练习册系列答案
相关题目
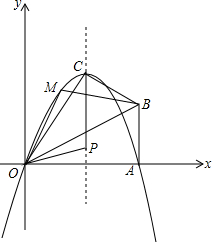（2013•武汉模拟）已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2，以O 为原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内，将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．
所示的等腰直角三角形BCD，点E在过A、C、D三点的圆上，且DE⊥BD，连结CE、AD．
