Question

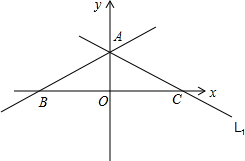
将直线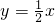向上平移4个单位，平移后的直线l与y轴交于A点，与x轴交于B点，直线l关于y轴对称的直线为l₁，求直线为l₁的解析式及直线l、l₁和x轴所围成的三角形外接圆圆心的坐标．

Answer 1

解：由已知得直线L的解析式为y=x+4
∴A（0，4）B（-8，0），
∴C（8，0），
∴解析式为y=-x+4；
过线段AB的中点E作其垂直平分线ED交y轴于D，如图：则D为三角形外接圆的圆心
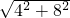AE=AB==×=2，
∵△AED∽△AOB，
∴

AD=10，OD=10-4=6
三角形外接圆的圆心D的坐标为（0，-6）
答；所求直线的解析式为y=-x+4；三角形外接圆的圆心D的坐标为（0，-6）．
分析：由已知条件易得直线L的解析式，从而求得A、B的坐标，根据对称可求得C的坐标，于是直线L₁可求；要确定其外接圆圆心D的位置，然后根据三角形相似可求出坐标．
点评：本题考查了一次函数的综合应用；认真观察图形，找着三角形外接圆的圆心后利用相似求解是正确解答本题的关键．