题目内容
 已知二次函数y=ax2+bx+c的图象如图:
已知二次函数y=ax2+bx+c的图象如图:
①对称轴方程是:______
②点A(x1,y1),B(x2,y2)是图象上的两个点,且x1<x2<1,则______
③求函数解析式.
解答:①由于抛物线与x轴的交点坐标为(-1,0),(4,0),
∴抛物线的对称轴为 ;
;
②由①知:抛物线的对称轴为x= >1,且抛物线的开口向上,
>1,且抛物线的开口向上,
因此当x1<x2<1时,y1>y2;
③由已知设二次函数的解析式为:y=a(x+1)(x-4);
因为点(0,4)在抛物线上,
所以-4=-4a,a=1;
∴二次函数的解析式为:y=(x+1)(x-4)=x2-3x-4.
分析:①通过抛物线与x轴的交点坐标可知其中点的横坐标即为对称轴x= ;
;
②根据函数的单调性可知:当x1<x2<1时,y1>y2;
③根据(-1,0),(4,0),(0,-4)三点的坐标,可用待定系数法求出抛物线的解析式.
点评:主要考查了用待定系数法求函数解析式的方法以及二次函数的图象性质.
∴抛物线的对称轴为
 ;
;②由①知:抛物线的对称轴为x=
 >1,且抛物线的开口向上,
>1,且抛物线的开口向上,因此当x1<x2<1时,y1>y2;
③由已知设二次函数的解析式为:y=a(x+1)(x-4);
因为点(0,4)在抛物线上,
所以-4=-4a,a=1;
∴二次函数的解析式为:y=(x+1)(x-4)=x2-3x-4.
分析:①通过抛物线与x轴的交点坐标可知其中点的横坐标即为对称轴x=
 ;
;②根据函数的单调性可知:当x1<x2<1时,y1>y2;
③根据(-1,0),(4,0),(0,-4)三点的坐标,可用待定系数法求出抛物线的解析式.
点评:主要考查了用待定系数法求函数解析式的方法以及二次函数的图象性质.

练习册系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
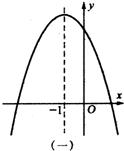 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
